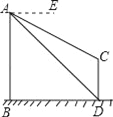
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
参考答案:
【答案】(1)两建筑物底部之间水平距离BD的长度为60米;
(2)建筑物CD的高度为(60﹣20![]() )米.
)米.
【解析】试题分析:
(1)由已知可判断△ABD是等腰直角三角形;
(2)过点A作DC延长线的垂线,垂足为点F,则在Rt△AFC,求出FC的长,再求CD的长.
试题解析:
(1)根据题意得:BD∥AE,
∴∠ADB=∠EAD=45°,
∵∠ABD=90°,
∴∠BAD=∠ADB=45°,
∴BD=AB=60,
∴两建筑物底部之间水平距离BD的长度为60米;
(2)延长AE、DC交于点F,
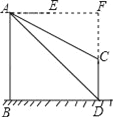
根据题意得四边形ABDF为正方形,
∴AF=BD=DF=60,
在Rt△AFC中,∠FAC=30°,
∴CF=AFtan∠FAC=60×![]() =20
=20![]() ,
,
又∵FD=60,
∴CD=60﹣20![]() ,
,
∴建筑物CD的高度为(60﹣20![]() )米.
)米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“校园手机”现象越来越受到社会的关注.小丽在“统计实习”活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的看法,统计整理并制作了如下的统计图:
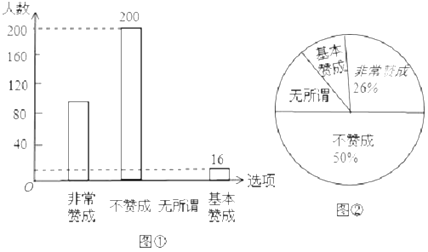
(1)求这次调查的家长总数及家长表示“无所谓”的人数,并补全图①;
(2)求图②中表示家长“无所谓”的圆心角的度数;
(3)若该学校有2000名家长,请根据该统计结果估算表示“基本赞成”的家长有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AD=2,E是AB的中点,将△BEC绕点B逆时针旋转90°后,点E落在CB的延长线上点F处,点C落在点A处.再将线段AF绕点F顺时针旋转90°得线段FG,连接EF,CG.
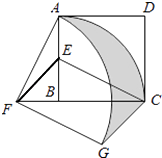
(1)求证:EF∥CG;
(2)求点C,点A在旋转过程中形成的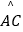 ,
, 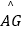 与线段CG所围成的阴影部分的面积.
与线段CG所围成的阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过点A(1,0),B(2,0),C(0,﹣2),直线x=m(m>2)与x轴交于点D.
(1)求二次函数的解析式;
(2)在直线x=m(m>2)上有一点E(点E在第四象限),使得E、D、B为顶点的三角形与以A、O、C为顶点的三角形相似,求E点坐标(用含m的代数式表示);
(3)在(2)成立的条件下,抛物线上是否存在一点F,使得四边形ABEF为平行四边形?若存在,请求出F点的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的两边长分别是4和7,则这个三角形的第三条边的长可能是( )
A. 12 B. 11 C. 8 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】红安卷烟厂生产的“龙乡”牌香烟盒里,装满大小均匀的20支香烟,打开烟盒的顶盖后,二十支香烟排列成三行,经测量,一支香烟的直径约为0.75cm,长约为8.4cm.
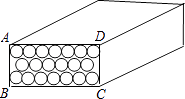
(1)试计算烟盒顶盖ABCD的面积(本小题计算结果不取近似值).
(2)制作这样一个烟盒至少需要多少面积的纸张(不计重叠粘合的部分,计算结果精确到0.1cm,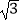 取1.73).
取1.73). -
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)当我们利用两种不同的方法计算同一图形的面积时,可以得到一个等式.例如,由图①,可得等式:(a+2b)(a+b)=a2+3ab+2b2.
(1)由图②,可得等式:__________________________;
(2)利用(1)中所得到的结论,解决下面的问题:
已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)利用图③中的纸片(足够多),画出一种拼图,使该拼图可用来验证等式:2a2+5ab+2b2=(2a+b)(a+2b);
(4)琪琪用2张边长为a的正方形,3张边长为b的正方形,5张边长分别为a,b的长方形纸片重新拼出一个长方形,那么该长方形较长的一条边长为________.

相关试题

