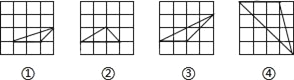
【题目】如图,点O是△ABC内任一点,点D,E,F分别为OA,OB,OC的中点,则图中相似三角形有( )

A. 1对 B. 2对 C. 3对 D. 4对
参考答案:
【答案】D
【解析】
根据点D,E,F分别为OA,OB,OC的中点,可得DE是△AOB的中位线,DF是△AOC的中位线,EF是△BOC的中位线,可得DE//AB,DF//AC,EF//BC,进而可判定△DOE∽△AOD, △DOF∽△AOC, △EOF∽△BOC,根据中位线性质可得![]() ,
,![]() ,
,
继而可得![]() ,可判定△DEF∽△ABC.
,可判定△DEF∽△ABC.
因为点D,E,F分别为OA,OB,OC的中点,
所以DE是△AOB的中位线,DF是△AOC的中位线,EF是△BOC的中位线,
所以DE//AB,DF//AC,EF//BC,
所以△DOE∽△AOD, △DOF∽△AOC, △EOF∽△BOC,
因为DE是△AOB的中位线,DF是△AOC的中位线,EF是△BOC的中位线,
所以![]() ,
,![]() ,
,
所以![]() ,
,
所以△DEF∽△ABC,
因此有四对相似三角形,
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是放在地面上的一个长方体盒子,其中AB=18cm,BC=12cm,BF=10cm,点M在棱AB上,且AM=6cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆有客房
 间供游客居住,当每间客房的定价为每天
间供游客居住,当每间客房的定价为每天 元时,客房恰好全部住满;如果每间客房每天的定价每增加
元时,客房恰好全部住满;如果每间客房每天的定价每增加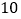 元,就会减少
元,就会减少 间客房出租.设每间客房每天的定价增加
间客房出租.设每间客房每天的定价增加 元,宾馆出租的客房为
元,宾馆出租的客房为 间.求:
间.求: 关于
关于 的函数关系式;
的函数关系式; 如果某天宾馆客房收入
如果某天宾馆客房收入 元,那么这天每间客房的价格是多少元?
元,那么这天每间客房的价格是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在正方形网格上有6个三角形:①△ABC;②△BCD;③△BDE;④△BFG;⑤△FGH;⑥△EFK.其中②~⑥中与①相似的是( )

A. ②③④ B. ③④⑤ C. ④⑤⑥ D. ②③⑥
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在大小为4×4的正方形网格中,是相似三角形的是( )
A. ①和② B. ②和③ C. ①和③ D. ②和④
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F。

(1)求证:△ABE≌△CAD;(2)求∠BFD的度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=6,BC=8.
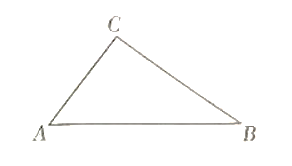
(1)用直尺和圆规作∠A的平分线,交BC于点D;(要求:不写作法,保留作图痕迹)
(2)求S△ADC: S△ADB的值.
相关试题

