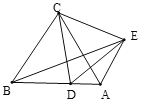
【题目】已知等边△ABC中,在射线BA上有一点D,连接CD,并以CD为边向上作等边△CDE,连接BE和AE.试判断下列结论:①AE=BD; ②AE与AB所夹锐夹角为60°;③当D在线段AB或BA延长线上时,总有∠BDE-∠AED=2∠BDC;④∠BCD=90°时,CE2+AD2=AC2+DE2 .正确的序号有( )

A. ①② B. ①②③ C. ①②④ D. ①②③④
参考答案:
【答案】C
【解析】
由∠BCD=∠ACD+60°,∠ACE=∠ACD+60°可得∠BCD=∠ACE,利用SAS可证明△BCD≌△ACE,可得AE=BD,①正确;∠CBD=∠CAE=60°,进而可得∠EAD=60°,②正确,当∠BCD=90°时,可得∠ACD=∠ADC=30°,可得AD=AC,即可得CE2+AD2=AC2+DE2 ,④正确;当D点在BA延长线上时,∠BDE-∠BDC=60°,根据△BCD≌△ACE可得∠AEC=∠BDC,进而可得∠BDC+∠AED=∠AEC+∠AED=∠CED=60°,即可证明∠BDE-∠BDC=∠BDC+∠AED,即∠BDE-∠AED=2∠BDC,当点D在AB上时可证明∠BDE-∠AED=120°,③错误,综上即可得答案.
∵∠BCA=∠DCE=60°,
∴∠BCA+∠ACD=∠DCE+∠ACD,
∴∠BCD=∠ACE,
又∵AC=BC,CE=CD,
∴△BCD≌△ACE,
∴AE=BD,∠CBA=∠CAE=60°,∠AEC=∠BDC,①正确,
∴∠BAE=120°,
∴∠EAD=60°,②正确,
∵∠BCD=90°,∠BCA=60°,
∴∠ACD=∠ADC=30°,
∴AC=AD,
∵CE=DE,
∴CE2+AD2=AC2+DE2,④正确,
当D点在BA延长线上时,∠BDE-∠BDC=60°,
∵∠AEC=∠BDC,
∴∠BDC+∠AED=∠AEC+∠AED=∠CED=60°,
∴∠BDE-∠BDC=∠BDC+∠AED
∴∠BDE-∠AED=2∠BDC,

如图,当点D在AB上时,
∵△BCD≌△∠ACE,
∴∠CAE=∠CBD=60°,
∴∠DAE=∠BAC+∠CAE=120°,
∴∠BDE-∠AED=∠DAE=120°,③错误
故正确的结论有①②④,
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的分式方程
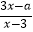 =
=  的解是非负数,那么a的取值范围是( )
的解是非负数,那么a的取值范围是( )
A.a>1
B.a≥1
C.a≥1且a≠9
D.a≤1 -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂去年底积压产品a件(a>0),今年预计每月销售产品2b件(b>0),同时每月可生产出产品b件,则产品积压量y(件)与今年开工时间t(月)的关系的图象应是( )
A.
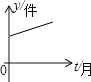 B.
B. 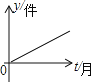 C.
C.  D.
D. 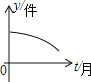
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AD=4,∠DAC=30°,点P、E分别在AC、AD上,则PE+PD的最小值是( )
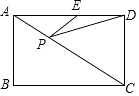
A.2
B.2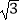
C.4
D.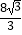
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=﹣x+2分别与x轴,y轴交于A,B两点,与双曲线y=
 交于E,F两点,若AB=2EF,则k的值是( )
交于E,F两点,若AB=2EF,则k的值是( )
A.﹣1
B.1
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,则反比例函数
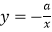 与一次函数y=bx﹣c在同一坐标系内的图象大致是( )
与一次函数y=bx﹣c在同一坐标系内的图象大致是( )
A.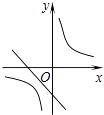
B.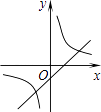
C.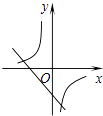
D.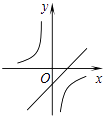
-
科目: 来源: 题型:
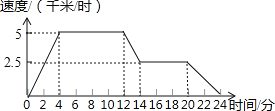
查看答案和解析>>【题目】某天放学后,小敏徒步回家,如图所示,反映了她的速度与时间的变化关系.
(1)请你根据图象填写下表:
时间/分
0
2
4
8
10
12
14
16
18
20
24
速度/(千米/时)
(2)根据图象或表格你能叙述一下小敏行走的情况吗?
相关试题

