【题目】某校有3600名学生，为了解全校学生的上学方式，该校数学兴趣小组以问卷调查的形式，随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类)，并将调查结果绘制成如下不完整的统计图．
（1）参与本次问卷调查的学生共有 人，其中选择D类的人数有 人；
（2）在扇形统计图中，求E类对应的扇形圆心角
的度数，并补全C对应的条形统计图；
（3）若将A、B、C．D．E这四类上学方式视为“绿色出行”，请估计该校选择“绿色出行”的学生人数．
【答案】（1）450，72；（2）
，答案见解析；（3）3456人．
【解析】
(1)用A的人数除以A所占总人数的百分比即得总的学生数；用D所占总人数的百分比乘以总的学生数即得D的学生人数；
(2)用100%减去A、B、C、D、F所占的百分比，得到E所占的百分比，然后再乘360°，即得到E类对应的圆心角；用20%乘以总的学生数即得到C类的学生数；
(3)用3600×4%即得到F类学生的人数，再用3600减去F类学生数即可.
(1)用A的人数除以A占总人数的比值：162÷36%=450(人)，
故本次问卷调查的学生共有450人，
其中D类的人数有：450×16%=72(人).
故答案为：共有460人，D类的人数有72人.
(2)E类学生占总人数的百分比为：1-36%-14%-20%-16%-4%=10%，
故E类对应的圆心角为：10%×360°=36°，
C类学生为：20%×450=90(人)，如下图所示：
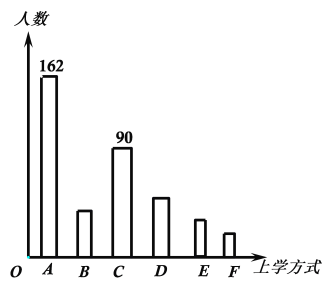
故答案为：36°.
(3)3600名学生中，F类所占的人数为：3600×4%=144(人)
故选择“绿色出行”的学生人数为：3600-144=3456(人)
故答案为：该校选择“绿色出行”的学生人数为3456(人)
科目：初中数学 来源： 题型：
【题目】如图，∠APB=30°，圆心在PB上的⊙O的半径为1cm，OP=3cm，若⊙O沿BP方向平移，当⊙O与PA相切时，圆心O平移的距离为_____cm．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在数轴上，点A、B分别表示数a、b，且|a＋6|＋|b－10|＝0，记AB＝|a－b|
(1) 求AB的值
(2) 如图，点P、Q分别从点A、B出发沿数轴向右运动，点P的速度是每秒4个单位长度，点Q的速度是每秒1个单位长度，点C从原点出发沿数轴向右运动，速度是每秒3个单位长度．经过多少秒，点C与点P、Q的距离相等？
(3) 在(2)的条件下，点M从对应－8的点出发沿数轴向左运动，速度是每秒4个单位长度，在运动过程中，MP＋MC－3MQ的值是否为定值？若是，求出其值，若不是，请说明理由
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】数轴上有A、B、C三点，分别表示有理数－26、－10、20，动点P从A出发，以每秒1个单位的速度向右移动，当P点运动到C点时运动停止．设点P移动时间为t秒
(1) 用含t的代数式表示P点对应的数；
(2) 当P点运动到B点时，点Q从A点出发，以每秒2个单位的速度向C点运动，Q点到达C点后，再立即以同样的速度返回A点；
① 用含t的代数式表示Q点在由A到C过程中对应的数；
② 当t＝___________时，动点P、Q到达同一位置（即相遇）；
③ 当PQ＝3时，求t的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知一次函数y=mx+n的图像与x轴交于点B，与反比例函数
(k﹥0)的图像交于点C，过点C作CH⊥x轴，点D是反比例函数图像上的一点，直线CD与x轴交于点A，若∠HCB=∠HCA，且BC=10，BA=16．
（1）若OA=11，求k的值；
（2）沿着x轴向右平移直线BC，若直线经过H点时恰好又经过点D，求一次函数函数y=mx+n的表达式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图都是由7个小立方体搭成的几何体，从不同方向看几何体，分别画出它们的主视图、左视图与俯视图，并在小正方形内填上表示该位置的小正方体的个数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD中，点E、F分别在边BC、CD上，连接AE、EF、AF，且∠EAF＝45°，下列结论：
①△ABE≌△ADF；
②∠AEB＝∠AEF；
③正方形ABCD的周长＝2△CEF的周长；
④S△ABE+S△ADF＝S△CEF，其中正确的是_____．（只填写序号）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】高新一中新图书馆在“校园书香四溢”活动中迎来了借书高潮，上周借书记录如下表：（超过100册的部分记为正，少于100册的部分记为负）
（1）上星期借书最多的一天比借书最少的一天多借出图书多少册？
（2）上星期平均每天借出多少册书？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
