搜索
【题目】如图，在菱形ABCD中，AB=5cm，∠ADC=120°，点E、F同时由A、C两点出发，分别沿AB．CB方向向点B匀速移动(到点B为止)，点E的速度为1cm/s，点F的速度为2cm/s，经过t秒△DEF为等边三角形，则t的值为( )
A.
B.
C.
D.
参考答案：
【答案】D
【解析】
由题意知道AE=t，CF=2t，连接BD，证明△DEB≌△DFC，得到EB=FC=2t，进而AB=AE+EB=3t=5，进而求出t的值.
解：连接DB，如下图所示，
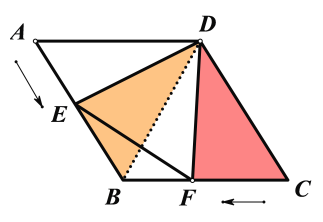
∵四边形ABCD为菱形，且∠ADC=120°，
∴∠CDB=60°
∴△CDB为等边三角形，∴DB=DC
又∵△DEF为等边三角形，∴∠EDF=60°，DE=DF
∴∠CDB=∠EDF
∴∠CDB-∠BDF=∠EDF-∠BDF
∴∠CDF=∠BDE
在△EDB和△FDC中：
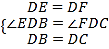，∴△EDB≌△FDC(SAS)
∴FC=BE=2t
∴AB=AE+EB=t+2t=3t=5
∴t=
.
故答案为：D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】数轴上有A、B、C三点，分别表示有理数－26、－10、20，动点P从A出发，以每秒1个单位的速度向右移动，当P点运动到C点时运动停止．设点P移动时间为t秒
(1) 用含t的代数式表示P点对应的数；
(2) 当P点运动到B点时，点Q从A点出发，以每秒2个单位的速度向C点运动，Q点到达C点后，再立即以同样的速度返回A点；
① 用含t的代数式表示Q点在由A到C过程中对应的数；
② 当t＝___________时，动点P、Q到达同一位置（即相遇）；
③ 当PQ＝3时，求t的值.
-
科目： 来源： 题型：
查看答案和解析>>【题目】若将一幅三角板按如图所示的方式放置，则下列结论中不正确的是( )
A. ∠1＝∠3 B. 如果∠2＝30°，则有AC∥DE
C. 如果∠2＝30°，则有BC∥AD D. 如果∠2＝30°，必有∠4＝∠C
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠C=90°，把△ABC绕AC边的中点M旋转后得△DEF，若直角顶点F恰好落在AB边上，且DE边交AB边于点G，若AC=4，BC=3，则AG的长为( )
A.
B.
C.
D.1 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD中，AB=
，E是对角线AC上的动点，以DE为边作正方形DEFG，H是CD的中点，连接GH，则GH的最小值为____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校有3600名学生，为了解全校学生的上学方式，该校数学兴趣小组以问卷调查的形式，随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类)，并将调查结果绘制成如下不完整的统计图．
（1）参与本次问卷调查的学生共有 人，其中选择D类的人数有 人；
（2）在扇形统计图中，求E类对应的扇形圆心角
的度数，并补全C对应的条形统计图；（3）若将A、B、C．D．E这四类上学方式视为“绿色出行”，请估计该校选择“绿色出行”的学生人数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,∠1+∠2=180°，∠3=∠B，试判断∠AED与∠C的大小关系，并证明你的结论.
∠C与∠AED相等，理由如下：
∵∠1+∠2=180°(已知),∠1+∠DFE=180°(邻补角定义)
∴∠2=___(___)，
∴AB∥EF(___)
∵∠3=___(___)
又∠B=∠3(已知)
∴∠B=___(等量代换)
∴DE∥BC(___)
∴∠C=∠AED(___).
相关试题
