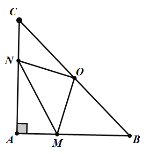
【题目】如图在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点.
(1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系.
(2)如果点M、N分别在线段AB、AC上移动,移动中保持AN=BM,请判断△OMN的形状,并证明你的结论.
(3)当点M、N分别在AB、AC上运动时,四边形AMON的面积是否发生变化?说明理由.
参考答案:
【答案】(1) OA=OB=OC;(2)等腰三角形;(3)不变.
【解析】
(1)由于△ABC是直角三角形,点O是BC的中点,根据直角三角形的性质:直角三角形斜边上的中线等于斜边的一半,故有OA=OB=OC=![]() BC;
BC;
(2)由于OA是等腰直角三角形的斜边上的中线,根据等腰直角三角形的性质知,∠CAO=∠B=45°,OA=OB,又有AN=MB,所以由SAS证得△AON≌△BOM可得:ON=OM ①∠NOA=∠MOB,于是有,∠NOM=∠AOB=90°,所以△OMN是等腰直角三角形.
(3)由全等三角形的面积相等和图中图形间的面积关系得到.
(1)∵在Rt△ABC中,∠BAC=90°,O为BC的中点,
∴OA=![]() BC=OB=OC,
BC=OB=OC,
即OA=OB=OC;
(2)△OMN是等腰直角三角形.理由如下:
连接AO
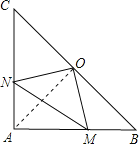
∵AC=AB,OC=OB
∴OA=OB,∠NAO=∠B=45°,
在△AON与△BOM中,
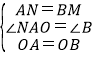 ,
,
∴△AON≌△BOM(SAS)
∴ON=OM,∠NOA=∠MOB
∴∠NOA+∠AOM=∠MOB+∠AOM
∴∠NOM=∠AOB=90°,
∴△OMN是等腰直角三角形;
(3)当点M、N分别在AB、AC上运动时,四边形AMON的面积不发生变化.理由如下:
M、N运动时始终有△AON≌△BOM,
故S四边形AMON=SAMO+SMBO=SABO=![]() SABC.
SABC.
-
科目: 来源: 题型:
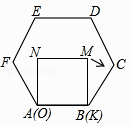
查看答案和解析>>【题目】已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作: 将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M间的距离可能是( )
A.1.4
B.1.1
C.0.8
D.0.5 -
科目: 来源: 题型:
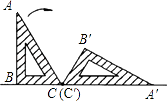
查看答案和解析>>【题目】如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C′的位置,若BC=12cm,则顶点A从开始到结束所经过的路径长为 cm.
-
科目: 来源: 题型:
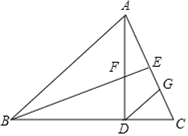
查看答案和解析>>【题目】如图,在△ABC中,AB=BC,AD⊥BC于点D,点E为AC中点且BE平分∠ABD,连接BE交AD于点F,且BF=AC,过点D作DG∥AB,交AC于点G.
求证:
(1)∠BAD=2∠DAC
(2)EF=EG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:通过小学的学习我们知道,分数可分为“真分数”和“假分数”,而假分数都可化为常分数,如:
 =
= 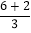 =2+
=2+  =2
=2  .我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.如
.我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.如 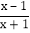 ,
,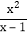 这样的分式就是假分式;再如:
这样的分式就是假分式;再如: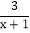 ,
,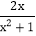 这样的分式就是真分式.类似的,假分式也可以化为带分式(即:整式与真分式的和的形式).如:
这样的分式就是真分式.类似的,假分式也可以化为带分式(即:整式与真分式的和的形式).如: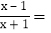
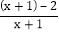 =1-
=1-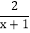 ;
; 解决下列问题:
(1)分式
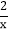 是 分式(填“真分式”或“假分式”);
是 分式(填“真分式”或“假分式”);(2)
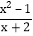 将假分式化为带分式;
将假分式化为带分式;(3)如果 x 为整数,分式
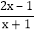 的值为整数,求所有符合条件的 x 的值.
的值为整数,求所有符合条件的 x 的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中有两点M(a,b),N(c,d),规定(a,b)⊕(c,d)=(a+c,b+d),则称点Q(a+c,b+d)为M,N的“和点”.若以坐标原点O与任意两点及它们的“和点”为顶点能构成四边形,则称这个四边形为“和点四边形”,现有点A(2,5),B(﹣1,3),若以O,A,B,C四点为顶点的四边形是“和点四边形”,则点C的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB∥CD,EF分别交AB、CD于G、F两点,射线FM平分∠EFD,将射线FM平移,使得端点F与点G重合且得到射线GN.若∠EFC=110°,则∠AGN的度数是( )

A. 120° B. 125° C. 135° D. 145°
相关试题

