【题目】珍珍与环环两人一起做游戏,游戏规则如下:每人从1,2,3,4,5,6,7,8中任意选择一个数字,然后两人各转动一次如图所示的转盘(转盘被分为面积相等的四个扇形),两人转出的数字之和等于谁事先选择的数,谁就获胜;若两人转出的数字之和不等于她们各自选择的数,就再做一次上述游戏,直到决出胜负.若环环事先选择的数是5,用列表法或画树状图的方法,求她获胜的概率.

参考答案:
【答案】![]()
【解析】试题分析:先根据题意用列表法将所有的情况列出来,进而得出所有等可能的情况以及结果是5的情况;
再运用概率公式即可求出小军获胜的概率.
试题解析:珍珍与环环转动的数字分别记为甲与乙,两人转动后得到的数字之和可列表如下:
甲 乙 | 1 | 2 | 3 | 4 |
1 | 2 | 3 | 4 | 5 |
2 | 3 | 4 | 5 | 6 |
3 | 4 | 5 | 6 | 7 |
4 | 5 | 6 | 7 | 8 |
由上表可以看出,转动两次转盘,可能出现的结果有16种,并且它们出现的可能性相等.
两次转动的点数之和为5(记为事件A)的结果共有4种
所以![]()
答:环环获胜的概率是![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.

(1)根据图象信息,当t= 分钟时甲乙两人相遇,甲的速度为 米/分钟,乙的速度为 米/分钟;
(2)图中点A的坐标为 ;
(3)求线段AB所直线的函数表达式;
(4)在整个过程中,何时两人相距400米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨,则每吨按政府补贴优惠价a元收费;若每月用水量超过14吨,则超过部分每吨按市场调节价b元收费.小刘家3月份用水10吨,交水费20元;4月份用水16吨,交水费35元.
(1)求每吨水的政府补贴优惠价和市场调节价分别是多少?
(2)设每月用水量为x吨,应交水费为y元,请写出y与x之间的函数关系式;
(3)小刘预计他家5月份用水不会超过22吨,那么小刘家5月份最多交多少元水费?
-
科目: 来源: 题型:
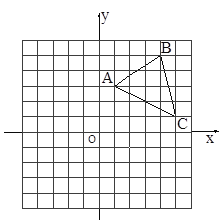
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(1,3),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点B1的坐标;
(2)画出△ABC绕原点O逆时针旋转90°后得到的△A2B2C2,并写出点C2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,直线y=8﹣2x与y轴交于点A,与x轴交于点B,直线y=x+b与y轴交于点C,与x轴交于点D,如果两直线交于点P,且AC:CO=3:5(AO>CO)

(1)求点A、B的坐标
(2)求直线y=x+b的函数解析式
(3)求四边形COBP的面积S
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
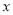 的一元二次方程
的一元二次方程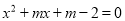 .
.(1)若此方程的一个根为1,求
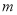 的值;
的值;(2)求证:不论
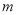 取何实数,此方程都有两个不相等的实数根.
取何实数,此方程都有两个不相等的实数根. -
科目: 来源: 题型:
查看答案和解析>>【题目】夏季来临,某饮品店老板大白计划下个月(2018年8月)每天制作新鲜水果冰淇淋800份销售。去年同期,这种冰淇淋每份的成本价为5元,售价为8元。该冰淇淋不含防腐剂,很受顾客的欢迎,但如果当天制作的冰淇淋未售出,新鲜水果就会腐败变质,饮品店就将承担冰淇淋制作成本的损失。根据大白去年的销售记录,得到去年同期该冰淇淋日销售量的频数分布表和频数分布直方图(不完整)如下:
2018年8月该冰淇淋日销售量频数分布表 2018年8月该冰淇淋日销售量频数分布直方图

由于今年水果涨价,该冰淇淋的制作成本提高了10%.大白计划今年冰淇淋还按8元/份销售.设下个月该冰淇淋的日销售量为m份(0<m800).

(1)请根据以上信息补全频数分布表和直方图,并标明相应数据;
(2)用含m的式子表示下个月销售该冰淇淋的日利润;
(3)大白认为,下个月该冰淇淋的销售状况将会与去年同期相差不多.
①请你通过计算帮助大白估计下个月销售该冰淇淋的日利润少于1200元的天数;
②为减少因当日冰淇淋未售出造成的损失,大白计划今年采取下班前打八折销售的方法,希望将剩余的冰淇淋售出,请你通过计算帮助大白估计下个月因销售该冰淇淋获得月利润的范围.
相关试题

