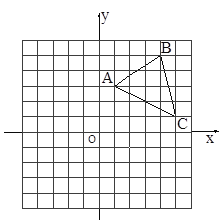
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(1,3),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点B1的坐标;
(2)画出△ABC绕原点O逆时针旋转90°后得到的△A2B2C2,并写出点C2的坐标.
参考答案:
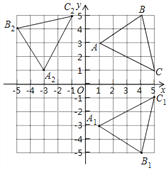
【答案】(1)作图见解析,B1(4,-5);(2)作图见解析,C2(-1,5)
【解析】试题分析:(1)分别找出A、B、C三点关于x轴的对称点,再顺次连接,然后根据图形写出B1点坐标即可;
(2)将△ABC中的各点A、B、C绕原点O旋转90°后,得到相应的对应点A2、B2、C2,连接各对应点即得△A2B2C2,然后根据图形写出C2点坐标即可.
试题解析:(1)如图所示,△A1B1C1即为所求,点B1的坐标为(4,﹣5);
(2)如图所示,△A2B2C2即为所求,点C2的坐标为(﹣1,5).
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数的图象如图所示,对称轴为x=1,给出下列结论:①abc<0;②b2>4ac;③4a+2b+c<0;④2a+b=0..其中正确的结论有:

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.

(1)根据图象信息,当t= 分钟时甲乙两人相遇,甲的速度为 米/分钟,乙的速度为 米/分钟;
(2)图中点A的坐标为 ;
(3)求线段AB所直线的函数表达式;
(4)在整个过程中,何时两人相距400米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨,则每吨按政府补贴优惠价a元收费;若每月用水量超过14吨,则超过部分每吨按市场调节价b元收费.小刘家3月份用水10吨,交水费20元;4月份用水16吨,交水费35元.
(1)求每吨水的政府补贴优惠价和市场调节价分别是多少?
(2)设每月用水量为x吨,应交水费为y元,请写出y与x之间的函数关系式;
(3)小刘预计他家5月份用水不会超过22吨,那么小刘家5月份最多交多少元水费?
-
科目: 来源: 题型:
查看答案和解析>>【题目】珍珍与环环两人一起做游戏,游戏规则如下:每人从1,2,3,4,5,6,7,8中任意选择一个数字,然后两人各转动一次如图所示的转盘(转盘被分为面积相等的四个扇形),两人转出的数字之和等于谁事先选择的数,谁就获胜;若两人转出的数字之和不等于她们各自选择的数,就再做一次上述游戏,直到决出胜负.若环环事先选择的数是5,用列表法或画树状图的方法,求她获胜的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,直线y=8﹣2x与y轴交于点A,与x轴交于点B,直线y=x+b与y轴交于点C,与x轴交于点D,如果两直线交于点P,且AC:CO=3:5(AO>CO)

(1)求点A、B的坐标
(2)求直线y=x+b的函数解析式
(3)求四边形COBP的面积S
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
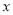 的一元二次方程
的一元二次方程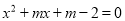 .
.(1)若此方程的一个根为1,求
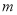 的值;
的值;(2)求证:不论
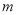 取何实数,此方程都有两个不相等的实数根.
取何实数,此方程都有两个不相等的实数根.
相关试题

