【题目】(2016·无锡中考)如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )

A. ![]() B. 2
B. 2![]() C. 3 D. 2
C. 3 D. 2![]()
参考答案:
【答案】A
【解析】∵∠C=90°,∠ABC=30°,AC=2,
∴AB=4,∠A=60°,
由勾股定理得,BC=![]() =
=![]() ,
,
由旋转的性质可知,CA=CA′,由∠A=60°,
∴△ACA′是等边三角形,
∴AA′=2,
∴A′B=2,
由旋转的性质可知,△B BC是等边三角形,
∴BB =![]() ,
,
∴BD=![]() ,
,
由勾股定理得,AD=![]() .
.
故选:A.
点睛: 本题考查旋转的性质、30度角的直角三角形性质、等边三角形的判定和性质、勾股定理等知识,解题的关键是证明△ACA1,△BCB1是等边三角形,属于中考常考题型.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某人购进一批苹果,到市场零售,已知卖出苹果数量x与售价y的关系如下表,写出用x表示y的关系式______.
数量x(千克)
2
3
4
5
售价y(元)
16.2
24.3
32.4
40.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一组数据2,3,x , 5,7的众数为7,则这组数据的中位数为 ( )
A.2
B.3
C.5
D.7 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中,AD∥BC,∠ABC=
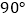 ,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )
,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )
A. 1个
B. 2个
C. 3个
D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.
(1)求证:△ADE≌△ABF;
(2)△ABF可以由△ADE绕旋转中心________点,按顺时针旋转________度得到;
(3)若BC=8,DE=6,求△AEF的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. x3+x=2x4 B. a2a3=a6
C. (﹣2x2)3=﹣8x6 D. (x+3y)(x﹣3y)=x2﹣3y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(2x2y)3(-3xy2)÷6xy
(2)2a2(3a2-2a+1)+4a3
相关试题

