【题目】如图,四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.
(1)求证:△ADE≌△ABF;
(2)△ABF可以由△ADE绕旋转中心________点,按顺时针旋转________度得到;
(3)若BC=8,DE=6,求△AEF的面积.

参考答案:
【答案】(1)见解析 (2)A 90 (3)50
【解析】试题分析: (1)根据正方形的性质得AD=AB,∠D=∠ABC=90°,然后利用“SAS”易证得△ADE≌△ABF;
(2)由于△ADE≌△ABF得∠BAF=∠DAE,则∠BAF+∠BAE=90°,即∠FAE=90°,根据旋转的定义可得到△ABF可以由△ADE绕旋转中心 A点,按顺时针方向旋转90度得到;
(3)先利用勾股定理可计算出AE=10,再根据△ABF可以由△ADE绕旋转中心 A点,按顺时针方向旋转90度得到AE=AF,∠EAF=90°,然后根据直角三角形的面积公式计算即可.
试题解析:
(1)证明:∵四边形ABCD为正方形,
∴AB=AD,∠ABF=∠ADE=90°.
∵DE=BF,
∴△ADE≌△ABF;
(2) ∵△ADE≌△ABF,
∴∠BAF=∠DAE,
而∠DAE+∠EAB=90°,
∴∠BAF+∠EAB=90°,即∠FAE=90°,
∴△ABF可以由△ADE绕旋转中心A点,按顺时针方向旋转90度得到;
故答案为A.90;
(3)在Rt△ADE中,
∵AD=BC=8,DE=6,
∴AE=10.
由题意可知AF=AE=10,∠EAF=90°,
∴S△AEF=![]() AE·AF=50.
AE·AF=50.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一组数据2,3,x , 5,7的众数为7,则这组数据的中位数为 ( )
A.2
B.3
C.5
D.7 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中,AD∥BC,∠ABC=
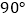 ,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )
,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )
A. 1个
B. 2个
C. 3个
D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016·无锡中考)如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )

A.
 B. 2
B. 2 C. 3 D. 2
C. 3 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. x3+x=2x4 B. a2a3=a6
C. (﹣2x2)3=﹣8x6 D. (x+3y)(x﹣3y)=x2﹣3y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(2x2y)3(-3xy2)÷6xy
(2)2a2(3a2-2a+1)+4a3
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016·毕节中考)如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.

相关试题

