【题目】某中学学生为了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类),并将调查的结果绘制成如下的两幅不完整的统计图.

请根据图中提供的信息,解答下面的问题:
(1)参加调查的学生共有 人,在扇形图中,表示“其他球类”的扇形的圆心角为 度;
(2)将条形图补充完整;
(3)若该校有2000名学生,则估计喜欢“篮球”的学生共有多少人呢?
参考答案:
【答案】(1)300、36;(2)喜欢足球的学生人数为90人;图详见解析;(3)800人
【解析】
(1)本题需根据喜欢乒乓球的人数和所占的百分比即可求出参加调查的学生总数,用360°乘以喜欢“其他球类”的学生所占的百分比即可得出圆心角的度数;
(2)本题需先求出喜欢足球的学生人数即可将条形图补充完整;
(3)本题需先求出喜欢“篮球”的学生所占的百分比即可得出该校喜欢“篮球”的学生人数.
解:(1)参加调查的学生共有60÷20%=300(人),
表示“其他球类”的扇形的圆心角为:![]() ,
,
故答案为:300,36;
(2)喜欢足球的学生人数为:300-120-60-30=90(人),条形图如图.
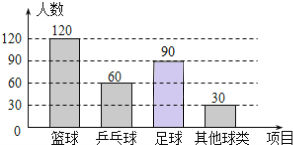
(3)喜欢“篮球”的学生共有:
![]() (人),
(人),
故答案为:800.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BC=5,∠A=80°,∠B=70°,把△ABC沿RS的方向平移到△DEF的位置,若CF=4,则下列结论中错误的是( )

A.BE=4
B.∠F=30°
C.AB∥DE
D.DF=5 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图△ABC的顶点坐标分别为A(-4,-3),B(0,-3),C(-2,1),如将B点向右平移2个单位后再向上平移4个单位到达B1点,若设△ABC的面积为S1 , △AB1C的面积为S2 , 则S1 , S2的大小关系为( )

A.S1>S2
B.S1=S2
C.S1<S2
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,已知A(﹣1,5),B(4,2),C(﹣1,0)三点.点A关于原点O的对称点A′,点B关于
中,已知A(﹣1,5),B(4,2),C(﹣1,0)三点.点A关于原点O的对称点A′,点B关于 轴的对称点为B′,点C关于
轴的对称点为B′,点C关于 轴的对称点为C′.
轴的对称点为C′.(1)A′的坐标为 ,B′的坐标为 ,C′的坐标为 .
(2)建立平面直角坐标系,描出以下三点A、B′、C′,并求△AB′C′的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点
 、
、 ,连接
,连接 .如果点
.如果点 在直线
在直线 上,且点
上,且点 到直线
到直线 的距离不大于1,那么称点
的距离不大于1,那么称点 是线段
是线段 的“临近点”.
的“临近点”.
(1)判断点
 是否是线段
是否是线段 的“临近点”,并说明理由;
的“临近点”,并说明理由;(2)若点
 是线段
是线段 的“临近点”.①求
的“临近点”.①求 的取值范围;②设直线
的取值范围;②设直线 与
与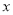 轴交于
轴交于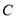 点,试用
点,试用 表达
表达 的面积
的面积 ,并求出
,并求出 的最大面积.
的最大面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学新建了一栋7层的教学大楼,每层楼有8间教室,进出这栋大楼共有八道门,其中四道正门大小相同,四道侧门大小也相同.安全检查中,对八道门进行了测试:当同时开启一道正门和两道侧门时,2分内可以通过560名学生;当同时开启一道正门和一道侧门时,4分内可以通过800名学生.
(1)平均每分内一道正门和一道侧门分别可以通过多少名学生?
(2)检查中发现,紧急情况时因学生拥挤,出门的效率将降低30%.安全检查规定:在紧急情况下全大楼的学生应在5分内通过这八道门安全撤离,假设这栋教学大楼每间教室最多有45名学生,问建造的这八道门是否符合安全规定?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 与直线
与直线 交于
交于 ,
, 两点,点
两点,点 是抛物线上
是抛物线上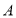 ,
, 之间的一个动点,过点
之间的一个动点,过点 分别作
分别作 轴、
轴、 轴的平行线与直线
轴的平行线与直线 交于点
交于点 ,
,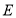 .
.
(1)求抛物线的解析式;
(2)若
 为
为 的中点,求
的中点,求 的长;
的长;(3)如图,以
 ,
, 为边构造矩形
为边构造矩形 ,设点
,设点 的坐标为
的坐标为 ,
,①请求出
 ,
, 之间的关系式;②求出矩形
之间的关系式;②求出矩形 的周长最大时,点
的周长最大时,点 的坐标.
的坐标.
相关试题

