【题目】如图1所示的晾衣架,支架主视图的基本图形是菱形,其示意图如图2,晾衣架伸缩时,点G在射线DP上滑动,∠CED的大小也随之发生变化,已知每个菱形边长均等于20cm,且AH=DE=EG=20cm.

(1)当∠CED=60°时,CD=________cm.
(2)当∠CED由60°变为120°时,点A向左移动了________cm(结果精确到0.1cm)(参考数据 ![]() ≈1.73).
≈1.73).
参考答案:
【答案】 20 43.9
【解析】试题分析:(1)证明△CED是等边三角形,即可求解;
(2)分别求得当∠CED是60°和120°,两种情况下AD的长,求差即可.
试题解析:(1)连接CD(图1),
∵CE=DE,∠CED=60°,
∴△CED是等边三角形,
∴CD=DE=20cm;
(2)根据题意得:AB=BC=CD,
当∠CED=60°时,AD=3CD=60cm,
当∠CED=120°时,过点E作EH⊥CD于H(图2),则∠CEH=60°,CH=HD,
在直角△CHE中,sin∠CEH=![]() ,
,
∴CH=20sin60°=20×![]() =10
=10![]() (cm),
(cm),
∴CD=20![]() cm,
cm,
∴AD=3×20![]() =60
=60![]() ≈103.9(cm),
≈103.9(cm),
∴103.9-60=43.9(cm),
即点A向左移动了43.9cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了尽快实施“脱贫致富奔小康”宏伟意图,某县扶贫工作队为朝阳沟村购买了一批苹果树苗和梨树苗,已知一棵苹果树苗比一棵梨树苗贵2元,购买苹果树苗的费用和购买梨树苗的费用分别是3500元和2500元.
(1)若两种树苗购买的棵数一样多,求梨树苗的单价;
(2)若两种树苗共购买1100棵,且购买两种树苗的总费用不超过6000元,根据(1)中两种树苗的单价,求梨树苗至少购买多少棵.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若规定两数a、b通过“※”运算,得到4ab,即a※b=4ab,例如2※6=4×2×6=48
(1)求3※5的值;
(2)求x※x+2※x-2※4=0中x的值;
(3)若无论x是什么数,总有a※x=x,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是等边三角形,过它的三个顶点分别作对边的平行线,则图中共有______个等边三角形.
是等边三角形,过它的三个顶点分别作对边的平行线,则图中共有______个等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D为等边△ABC边BC上一点,DE⊥AB于E,若BD:CD=2:1,DE=2
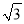 , 求AE.
, 求AE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题呈现:我们知道反比例函数y=
 (x>0)的图象是双曲线,那么函数y=
(x>0)的图象是双曲线,那么函数y= +n(k、m、n为常数且k≠0)的图象还是双曲线吗?它与反比例函数y=
+n(k、m、n为常数且k≠0)的图象还是双曲线吗?它与反比例函数y= (x>0)的图象有怎样的关系呢?让我们一起开启探索之旅……
(x>0)的图象有怎样的关系呢?让我们一起开启探索之旅……探索思考:我们可以借鉴以前研究函数的方法,首先探索函数y=
 的图象.
的图象.(1)填写下表,并画出函数y=
 的图象.
的图象.①列表:
x
…
﹣5
﹣3
﹣2
0
1
3
…
y
…
…
②描点并连线.
(2)观察图象,写出该函数图象的两条不同类型的特征:
① ② ;
理解运用:函数y=
 的图象是由函数y=
的图象是由函数y= 的图象向 平移 个单位,其对称中心的坐标为 .
的图象向 平移 个单位,其对称中心的坐标为 .灵活应用:根据上述画函数图象的经验,想一想函数y=
 +2的图象大致位置,并根据图象指出,当x满足 时,y≥3.
+2的图象大致位置,并根据图象指出,当x满足 时,y≥3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小敏在测量学校一幢教学楼AB的高度时,她先在点C测得教学楼的顶部A的仰角为30°,然后向教学楼前进12米到达点D,又测得点A的仰角为45°.请你根据这些数据,求出这幢教学楼AB的高度.
(结果精确到0.1米,参考数据:
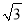 ≈1.73)
≈1.73)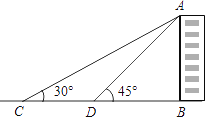
相关试题

