【题目】如图,已知AD为△ABC的高,AD=BC,以AB为底边作等腰Rt△ABE,EF∥AD,交AC于F,连ED,EC,有以下结论:①△ADE≌△BCE;②CE⊥AB;③BD=2EF;④S△BDE=S△ACE,其中正确的是( )

A.①②③B.②④C.①③D.①③④
参考答案:
【答案】D
【解析】
①易证∠CBE=∠DAE,即可求证:△ADE≌△BCE;
②根据①结论可得∠AEC=∠DEB,即可求得∠AED=∠BEG,即可解题;
③证明△AEF≌△BED即可;
④易证△FDC是等腰直角三角形,则CE=EF,S△AEF=S△ACE,由△AEF≌△BED,可知S△BDE=S△ACE,所以S△BDE=S△ACE.
如图延长CE交AD于K,交AB于H.设AD交BE于O.
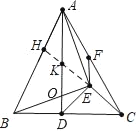
∵∠ODB=∠OEA,∠AOE=∠DOB,
∴∠OAE=∠OBD,
∵AE=BE,AD=BC,
∴△ADE≌△BCE,故①正确,
∴∠AED=∠BEC,DE=EC,
∴∠AEB=∠DEC=90°,
∴∠ECD=∠ABE=45°,
∵∠AHC=∠ABC+∠HCB=90°+∠EBC>90°,
∴EC不垂直AB,故②错误,
∵∠AEB=∠HED,
∴∠AEK=∠BED,
∵AE=BE,∠KAE=∠EBD,
∴△KAE≌△DBE,
∴BD=AK,
∵△DCK是等腰直角三角形,DE平分∠CDK,
∴EC=EK,
∵EF∥AK,
∴AF=FC,
∴AK=2EF,
∴BD=2EF,故③正确,
∵EK=EC,
∴S△AKE=S△AEC,
∵△KAE△DBE,
∴S△KAE=S△BDE,
∴S△BDE=S△AEC,故④正确.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】庆元大道两侧需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率,该绿化组完成的绿化面积S(单位m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
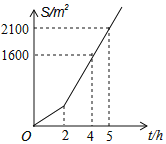
A. 200B. 300C. 400D. 500
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,DE⊥AC于E,
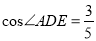 ,AB=3,
,AB=3,(1)求AD的值;
(2)直接写出
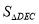 的值是_____________.
的值是_____________.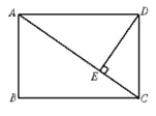
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了测量出楼房AC的高度,从距离楼底C处60
 米的点D(点D与楼底C在同一水平上)出发,沿斜面坡度为i=l:
米的点D(点D与楼底C在同一水平上)出发,沿斜面坡度为i=l: 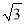 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53
的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53 ,求楼房AC的高度(参考数据:sin53
,求楼房AC的高度(参考数据:sin53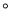 =
=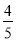 , cos53
, cos53 =
= , tan53
, tan53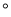 =
=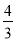 ,
, 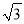 ≈1.732,结果精确到0.1米)
≈1.732,结果精确到0.1米)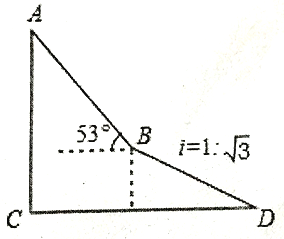
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一直角坐标系中,函数
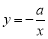 与
与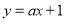
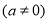 的图象可能是( )
的图象可能是( )A.
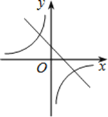 B.
B. 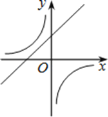 C.
C. 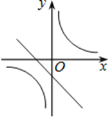 D.
D. 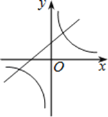
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的高,
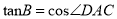 .
.(1)求证:AC=BD;
(2)若
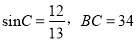 ,直接写出AD的长是__________.
,直接写出AD的长是__________.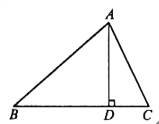
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数y=
 的图象与直线y=﹣x+b都经过点A(1,4),且该直线与x轴的交点为B.
的图象与直线y=﹣x+b都经过点A(1,4),且该直线与x轴的交点为B.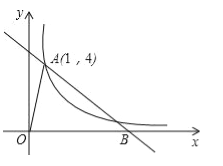
(1)求反比例函数和直线的解析式;
(2)求△AOB的面积.
相关试题

