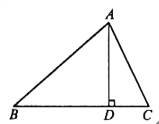
【题目】如图,在△ABC中,AD是BC边上的高, ![]() .
.
(1)求证:AC=BD;
(2)若![]() ,直接写出AD的长是__________.
,直接写出AD的长是__________.
参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:
(1)由AD是△ABC中BC边上的高,可得∠ADB=∠ADC=90°,结合tanB=cos∠DAC可得![]() 即可得到AC=BD;
即可得到AC=BD;
(2)由sinC=![]() ,若设AD=12x,则AC=13x,由(1)中结论AC=BD可得BD=13x,在Rt△ADC中可得CD=5x,即可得到BC=BD+CD=18x=34,由此可得x=
,若设AD=12x,则AC=13x,由(1)中结论AC=BD可得BD=13x,在Rt△ADC中可得CD=5x,即可得到BC=BD+CD=18x=34,由此可得x=![]() ,则AD=12x=
,则AD=12x=![]() .
.
试题解析:
(1)∵AD是△ABC中BC边上的高,
∴∠ADB=∠ADC=90°,
∴tanB=![]() ,cos∠DAC=
,cos∠DAC=![]() ,
,
又∵tanB=cos∠DAC,
∴![]() ,
,
∴AC=BD;
(2)∵sinC=![]() ,
,
∴若设AD=12x,则AC=13x,
∴在Rt△ADC中,CD=5x,
∵AC=BD,
∴BD=13x,
∴BC=BD+CD=18x,
又∵BC=34,
∴18x=34,解得:x=![]() ,
,
∴AD=12x=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了测量出楼房AC的高度,从距离楼底C处60
 米的点D(点D与楼底C在同一水平上)出发,沿斜面坡度为i=l:
米的点D(点D与楼底C在同一水平上)出发,沿斜面坡度为i=l: 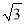 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53
的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53 ,求楼房AC的高度(参考数据:sin53
,求楼房AC的高度(参考数据:sin53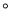 =
=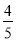 , cos53
, cos53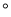 =
= , tan53
, tan53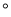 =
=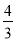 ,
, 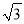 ≈1.732,结果精确到0.1米)
≈1.732,结果精确到0.1米)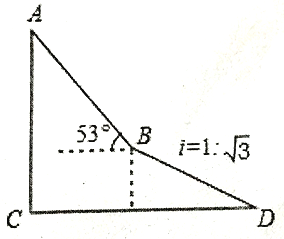
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD为△ABC的高,AD=BC,以AB为底边作等腰Rt△ABE,EF∥AD,交AC于F,连ED,EC,有以下结论:①△ADE≌△BCE;②CE⊥AB;③BD=2EF;④S△BDE=S△ACE,其中正确的是( )

A.①②③B.②④C.①③D.①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一直角坐标系中,函数
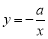 与
与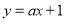
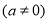 的图象可能是( )
的图象可能是( )A.
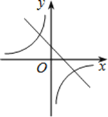 B.
B. 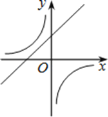 C.
C. 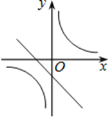 D.
D. 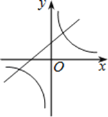
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数y=
 的图象与直线y=﹣x+b都经过点A(1,4),且该直线与x轴的交点为B.
的图象与直线y=﹣x+b都经过点A(1,4),且该直线与x轴的交点为B.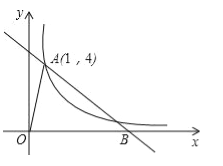
(1)求反比例函数和直线的解析式;
(2)求△AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=4,∠BAC=120°,M是BC的中点,点E是AB边上的动点,点F是线段BM上的动点,则ME+EF的最小值等于____.
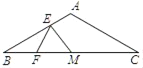
-
科目: 来源: 题型:
查看答案和解析>>【题目】从一副52张(没有大小王)的扑克中,每次抽出1张,然后放回洗匀再抽,在实验中得到下列表中部分数据:
实验次数
40
80
120
160
200
240
280
320
360
400
出现方块的次数
11
18
a
40
49
63
68
80
91
100
出现方块的频率
27.5%
22.5%
25%
25%
24.5%
26.25%
24.3%
b
25%
25%
(1)填空a= ,b= ;
(2)从上面的图表中可以估计出现方块的概率是 ;
(3)将这幅扑克中的所有方块(即从方块1到方块13,共13张)取出,将它们背面朝上重新洗牌后,从中摸出一张,若摸出的这张牌面数字为奇数,则甲方贏,若摸出的这张牌的牌面数字是偶数,则乙方赢,你认为这个游戏对双方是公平的吗说明理由.
相关试题

