【题目】在区间[﹣1,3]上随机取一个数x,若x满足|x|<m的概率为0.75,则m=( )
A.0
B.1
C.2
D.3
参考答案:
【答案】C
【解析】解:∵区间[﹣1,3]的区间长度为3﹣(﹣1)=4, ∴随机地取一个数x,若x满足|x|≤m的概率为0.75,
则满足条件的区间长度为4×0.75=3.
因此x所在的区间为[﹣1,2],
∵m>0,得|x|≤m的解集为{m|﹣m≤x≤m}=[﹣m,m],
∴[﹣m,m]与[﹣1,3]的交集为[﹣1,2]时,可得m=2.
故选:C.
【考点精析】通过灵活运用几何概型,掌握几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电视台用如下图所示的图像向观察描绘了一周之内日平均温度的变化情况:
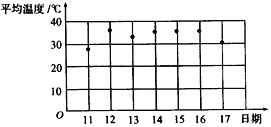
(1)这一周哪一天的日平均温度最低?大约是多少度?哪一天的平均温度最高?大约是多少度?你能用有序数对分别表示它们吗?
(2)14、15、16日的日平均温度有什么关系?
(3)说一说这一周日平均温度是怎样变化的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,正确的是( )
A. 平行四边形的对角线相等 B. 矩形的对角线互相垂直
C. 菱形的对角线互相垂直且平分 D. 菱形的对角线相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】植树节期间,某单位欲购进A、B两种树苗,若购进A种树苗3棵,B种树苗5棵,需2100元,若购进A种树苗4棵,B种树苗10棵,需3800元.
(1)求购进A、B两种树苗的单价;
(2)若该单位准备用不多于8000元的钱购进这两种树苗共30棵,求A种树苗至少需购进多少棵?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形A1B1C1是由三角形ABC平移后得到的,已知三角形ABC中任意一点P(x0,y0)经平移后对应点为P1(x0-6,y0-2).
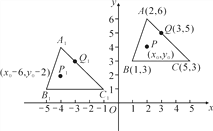
(1)已知A(2,6),B(1,3),C(5,3),Q(3,5),请写出A1,B1,C1,Q1的坐标;
(2)试说明三角形A1B1C1是如何由三角形ABC得到的?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了抓住梵净山文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】某商品原价为50元,连续两次涨价x%后售价为60元,则下面所列方程正确的是( )
A.50(1+x)2=60B.50(1+x%)2=60
C.(50+x%)2=60D.50(1+2x2)=60
相关试题

