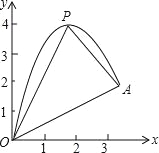
【题目】如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=﹣x2+4x刻画,斜坡可以用一次函数y=![]() x刻画.
x刻画.
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标;
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标.
参考答案:
【答案】(1)最高点P的坐标为(2,4);(2)点A的坐标为(![]() ,
,![]() );(3)
);(3)![]() ;(4)点M的坐标为(
;(4)点M的坐标为(![]() ,
,![]() ).
).
【解析】
试题分析:(1)利用配方法抛物线的一般式化为顶点式,即可求出二次函数图象的最高点P的坐标;
(2)联立两解析式,可求出交点A的坐标;
(3)作PQ⊥x轴于点Q,AB⊥x轴于点B.根据S△POA=S△POQ+S△梯形PQBA﹣S△BOA,代入数值计算即可求解;
(4)过P作OA的平行线,交抛物线于点M,连结OM、AM,由于两平行线之间的距离相等,根据同底等高的两个三角形面积相等,可得△MOA的面积等于△POA的面积.设直线PM的解析式为y=![]() x+b,将P(2,4)代入,求出直线PM的解析式为y=
x+b,将P(2,4)代入,求出直线PM的解析式为y=![]() x+3.再与抛物线的解析式联立,得到方程组
x+3.再与抛物线的解析式联立,得到方程组 ,解方程组即可求出点M的坐标.
,解方程组即可求出点M的坐标.
试题解析:(1)由题意得,y=﹣x2+4x=﹣(x﹣2)2+4,
故二次函数图象的最高点P的坐标为(2,4);
(2)联立两解析式可得: ,解得:
,解得:![]() ,或
,或![]() .
.
故可得点A的坐标为(![]() ,
,![]() );
);
(3)如图,作PQ⊥x轴于点Q,AB⊥x轴于点B.

S△POA=S△POQ+S△梯形PQBA﹣S△BOA
=![]() ×2×4+
×2×4+![]() ×(
×(![]() +4)×(
+4)×(![]() ﹣2)﹣
﹣2)﹣![]() ×
×![]() ×
×![]()
=4+![]() ﹣
﹣![]()
=![]() ;
;
(4)过P作OA的平行线,交抛物线于点M,连结OM、AM,则△MOA的面积等于△POA的面积.
设直线PM的解析式为y=![]() x+b,
x+b,
∵P的坐标为(2,4),
∴4=![]() ×2+b,解得b=3,
×2+b,解得b=3,
∴直线PM的解析式为y=![]() x+3.
x+3.
由 ,解得
,解得![]() ,
, ,
,
∴点M的坐标为(![]() ,
,![]() ).
).

-
科目: 来源: 题型:
查看答案和解析>>【题目】比-2大1的数是( )
A.-3B.-1C.3D.1
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,正确的个数是( )
①若三条线段的比为1:1:
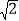 ,则它们组成一个等腰直角三角形;②两条对角线相等的平行四边形是矩形;③对角线互相垂直的四边形是菱形;④1,
,则它们组成一个等腰直角三角形;②两条对角线相等的平行四边形是矩形;③对角线互相垂直的四边形是菱形;④1,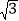 ,2是一组勾股数;⑤命题“若两个实数相等,则它们的平方相等”的逆命题成立⑥一次函数
,2是一组勾股数;⑤命题“若两个实数相等,则它们的平方相等”的逆命题成立⑥一次函数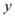 =kx+b,若k>0,b<0,那么它的图象过第一、二、三象限;⑦函数y=-6x+3是一次函数,且y随着x的增大而减小;
=kx+b,若k>0,b<0,那么它的图象过第一、二、三象限;⑦函数y=-6x+3是一次函数,且y随着x的增大而减小;A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
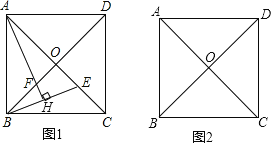
查看答案和解析>>【题目】如图,已知正方形ABCD,AC、BD相交于点O,E为AC上一点,AH⊥EB交EB于点H,AH交BD于点F.
(1)若点E在图1的位置,判断OE与OF的数量关系,并证明你的结论;
(2)若点E在AC的延长线上,请在图2中按题目要求补全图形,判断OE与OF的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2﹣2x+4化为y=a(x﹣h)2+k的形式,下列正确的是( )
A.y=(x﹣1)2+2
B.y=(x﹣1)2+3
C.y=(x﹣2)2+2
D.y=(x﹣2)2+4 -
科目: 来源: 题型:
查看答案和解析>>【题目】从2017年起,昆明将迎来“高铁时代”,这就意味着今后昆明的市民外出旅行的路程与时间将大大缩短,但也有不少游客根据自己的喜好依然选择乘坐普通列车;已知从昆明到某市的高铁行驶路程是400千米,普通列车的行驶路程是高铁行驶路程的1.3倍,请完成以下问题:(1)普通列车的行驶路程为________千米;(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求普通列车和高铁的平均速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列四个命题:①相等的角是对顶角;②两条直线被第三条直线所截,同位角相等;③等角的邻补角相等;④垂直于同一条直线的两条直线互相平行.其中真命题的个数为( )
A.1
B.2
C.3
D.4
相关试题

