搜索
【题目】如图，已知直线y＝x与反比例函数y＝
（x＞0）图象交于A，过点A作AC⊥x轴，垂足为C，一次函数y＝kx+b的图象经过点A，与y轴的正半轴交于B．
（1）求点A的坐标；
（2）若四边形ABOC的面积为3，求一次函数y＝kx+b的表达式．
参考答案：
【答案】（1）点A的坐标为（2，2）；（2）y＝
x+1．
【解析】
（1）解析式联立，解方程组可求点A的坐标；
（2）根据梯形的面积公式可求点B的坐标，再根据待定系数法可求一次函数y=kx+b的表达式．
解：（1）∵直线y＝x与反比例函数y＝
（x＞0）图象交于A，
得：
∴解得
或
（舍），
∴点A的坐标为（2，2）；
（2）∵四边形ABOC的面积是3，
∴
即 
解得OB＝1，
∴点B的坐标为（0，1），
依题意有
，
解得
．
故一次函数y＝kx+b的表达式为y＝x+1．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，直线AB∥CD
（1）如图1，点E在直线BD的左侧，猜想∠ABE、∠CDE、∠BED的数量关系，并证明你的结论；
（2）如图2，点E在直线BD的左侧，BF、DF分别平分∠ABE、∠CDE，猜想∠BFD和∠BED的数量关系，并证明你的结论；
（3）如图3，点E在直线BD的右侧，BF、DF分别平分∠ABE、∠CDE；那么第（2）题中∠BFD和∠BED的数量关系的猜想是否仍成立？如果成立，请证明；如果不成立，请写出你的猜想，并证明．
-
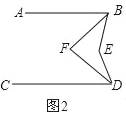
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，有若干个整数点(横、纵坐标均为整数)，其顺序按图中方向排列，如(1，0)，(2，0)，(2，1)，(3，1)，(3，0)…… 根据这个规律探索可得，第50个点的坐标为（ ）
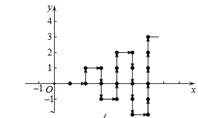
A. (10，－5)B. (10，－1) C. (10，0) D. (10，1）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正六边形A1B1C1D1E1F1的边长为1，它的六条对角线又围成一个正六边形A2B2C2D2E2F2 ， 如此继续下去，则正六边形A4B4C4D4E4F4的面积是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商店销售A型和B型两种电脑，其中A型电脑每台的利润为400元，B型电脑每台的利润为500元．该商店计划再一次性购进两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的2倍，设购进A型电脑x台，这100台电脑的销售总利润为y元．
（1）求y关于x的函数关系式；
（2）该商店购进A型、B型电脑各多少台，才能使销售总利润最大，最大利润是多少？
（3）实际进货时，厂家对A型电脑出厂价下调a（0＜a＜200）元，且限定商店最多购进A型电脑60台，若商店保持同种电脑的售价不变，请你根据以上信息，设计出使这100台电脑销售总利润最大的进货方案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线m经过A（4，0）、B（3，﹣
），直线n经过原点且与直线m相交于D，D点的横坐标为﹣2．（1）求直线m、n的表达式；
（2）求△OBD的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明根据学习函数的经验，对函数y＝|x|+2的图象与性质进行了研究，下面是小明的研究过程，请补充完成．
（1）函数y＝|x|+2的自变量x的取值范围是 ；
（2）列表，把表格填写完整：
x
……
﹣2
﹣1
0
1
2
……
y
……
……
（3）在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点，并画出该函数的图象；
（4）写出该函数的两条性质．
相关试题
