【题目】小明根据学习函数的经验,对函数y=|x|+2的图象与性质进行了研究,下面是小明的研究过程,请补充完成.
(1)函数y=|x|+2的自变量x的取值范围是 ;
(2)列表,把表格填写完整:
x | …… | ﹣2 | ﹣1 | 0 | 1 | 2 | …… |
y | …… |
|
|
|
|
| …… |
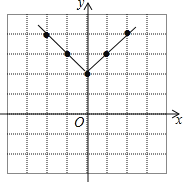
(3)在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)写出该函数的两条性质.

参考答案:
【答案】(1)任意实数;(2)4,3,2,3,4;(3)见解析;(4)函数的最小值为2,当x>0,y随x的增大而增大.(答案不唯一).
【解析】
(1)根据一次函数的性质即可得出结论;
(2)把x的值代入函数解析式,求出y的值即可;
(3)在坐标系内描出各点,再顺次连接即可;
(4)根据函数图象即可得出结论.
解:(1)∵x无论为何值,函数均有意义,
∴x为任意实数.
故答案为:任意实数;
(2)填写表格:
x | …… | ﹣2 | ﹣1 | 0 | 1 | 2 | …… |
y | …… | 4 | 3 | 2 | 3 | 4 | …… |
故答案为:4,3,2,3,4;
(3)如图所示;
(4)由函数图象可知,函数的最小值为2,当x>0,y随x的增大而增大.(答案不唯一).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=x与反比例函数y=
 (x>0)图象交于A,过点A作AC⊥x轴,垂足为C,一次函数y=kx+b的图象经过点A,与y轴的正半轴交于B.
(x>0)图象交于A,过点A作AC⊥x轴,垂足为C,一次函数y=kx+b的图象经过点A,与y轴的正半轴交于B.(1)求点A的坐标;
(2)若四边形ABOC的面积为3,求一次函数y=kx+b的表达式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售A型和B型两种电脑,其中A型电脑每台的利润为400元,B型电脑每台的利润为500元.该商店计划再一次性购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y关于x的函数关系式;
(2)该商店购进A型、B型电脑各多少台,才能使销售总利润最大,最大利润是多少?
(3)实际进货时,厂家对A型电脑出厂价下调a(0<a<200)元,且限定商店最多购进A型电脑60台,若商店保持同种电脑的售价不变,请你根据以上信息,设计出使这100台电脑销售总利润最大的进货方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线m经过A(4,0)、B(3,﹣
 ),直线n经过原点且与直线m相交于D,D点的横坐标为﹣2.
),直线n经过原点且与直线m相交于D,D点的横坐标为﹣2.(1)求直线m、n的表达式;
(2)求△OBD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一个边长不定的正方形ABCD,它的两个相对的顶点A,C分别在边长为1的正六边形一组平行的对边上,另外两个顶点B,D在正六边形内部(包括边界),则正方形边长a的取值范围是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣2x+4与x轴、y轴分别交于A、B两点,P是直线AB上的一个动点,点C的坐标为(﹣4,0),PC交y轴点于D,O是原点.
(1)求△AOB的面积;
(2)线段AB上存在一点P,使△DOC≌△AOB,求此时点P的坐标;
(3)直线AB上存在一点P,使以P、C、O为顶点的三角形面积与△AOB面积相等,求出P点的坐标.

-
科目: 来源: 题型:
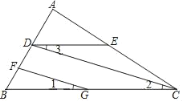
查看答案和解析>>【题目】完成下面的证明
(1)如图,FG∥CD,∠1=∠3,∠B=50°,求∠BDE的度数.
解:∵FG∥CD(已知)
∴∠2=
又∵∠1=∠3,
∴∠3=∠2(等量代换)
∴BC∥
∴∠B+ =180°
又∵∠B=50°
∴∠BDE= .
相关试题

