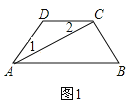
【题目】(1)、如图,AC平分∠DAB,∠1=∠2,试说明AB与CD的位置关系,并予以证明;
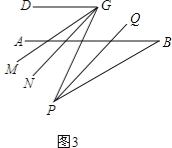
(2)、如图,在(1)的条件下,AB的下方两点E,F满足:BF平分∠ABE,CF 平分∠DCE,若∠CFB=20°,∠DCE=70°,求∠ABE的度数
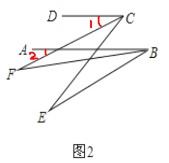
(3)、在前面的条件下,若P是BE上一点;G是CD上任一点,PQ平分∠BPG,PQ∥GN,GM平分∠DGP,下列结论:①∠DGP﹣∠MGN的值不变;②∠MGN 的度数不变.可以证明,只有一个是正确的,请你作出正确的选择并求值.

参考答案:
【答案】(1)、AB∥CD;理由见解析;(2)、30°;(3)、①∠DGP﹣∠MGN的值随∠DGP的变化而变化;②∠MGN的度数为15°不变;证明过程见解析.
【解析】
试题分析:(1)、根据角平分线得出∠1=∠CAB,从而得出∠2=∠CAB,从而说明平行线;(2)、根据角平分线的性质得出∠DCF=![]() ∠DCE=35°,∠ABE=2∠ABF,根据CD∥AB得出∠2=∠DCF=35°,根据∠2=∠CFB+∠ABF,∠CFB=20°得出∠ABF和∠ABE的度数;(3)、根据三角形外角性质得出∠1=∠BPG+∠B,根据角平分线的性质得出∠GPQ=
∠DCE=35°,∠ABE=2∠ABF,根据CD∥AB得出∠2=∠DCF=35°,根据∠2=∠CFB+∠ABF,∠CFB=20°得出∠ABF和∠ABE的度数;(3)、根据三角形外角性质得出∠1=∠BPG+∠B,根据角平分线的性质得出∠GPQ=![]() ∠BPG,∠MGP=
∠BPG,∠MGP=![]() ∠DGP,根据AB∥CD得出∠MGP=
∠DGP,根据AB∥CD得出∠MGP=![]() (∠BPG+∠B),根据PQ∥GN得出∠NGP=∠GPQ=
(∠BPG+∠B),根据PQ∥GN得出∠NGP=∠GPQ=![]() ∠BPG,从而根据∠MGN=∠MGP﹣∠NGP=
∠BPG,从而根据∠MGN=∠MGP﹣∠NGP=![]() ∠B,从而得出答案.
∠B,从而得出答案.
试题解析:(1)、AB∥CD.
∵AC平分∠DAB, ∴∠1=∠CAB, ∵∠1=∠2, ∴∠2=∠CAB, ∴AB∥CD;
(2)、如图2, ∵BF平分∠ABE,CF平分∠CDE, ∴∠DCF=![]() ∠DCE=35°,∠ABE=2∠ABF, ∵CD∥AB,
∠DCE=35°,∠ABE=2∠ABF, ∵CD∥AB,
∴∠2=∠DCF=35°, ∵∠2=∠CFB+∠ABF,∠CFB=20°, ∴∠ABF=15°, ∴∠ABE=2∠ABF=30°
(3)、如图3,根据三角形的外角性质,∠1=∠BPG+∠B, ∵PQ平分∠BPG,GM平分∠DGP,
∴∠GPQ=![]() ∠BPG,∠MGP=
∠BPG,∠MGP=![]() ∠DGP, ∵AB∥CD, ∴∠1=∠DGP, ∴∠MGP=
∠DGP, ∵AB∥CD, ∴∠1=∠DGP, ∴∠MGP=![]() (∠BPG+∠B),
(∠BPG+∠B),
∵PQ∥GN, ∴∠NGP=∠GPQ=![]() ∠BPG, ∴∠MGN=∠MGP﹣∠NGP=
∠BPG, ∴∠MGN=∠MGP﹣∠NGP=![]() (∠BPG+∠B)﹣
(∠BPG+∠B)﹣![]() ∠BPG=
∠BPG=![]() ∠B,
∠B,
根据前面的条件,∠B=30°, ∴∠MGN=![]() ×30°=15°,
×30°=15°,
∴①∠DGP﹣∠MGN的值随∠DGP的变化而变化;②∠MGN的度数为15°不变.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在“五一”黄金周期间,小明、小亮等同学随家人一同到章怀山游玩,下图是购门票时,小明与他爸爸的对话.
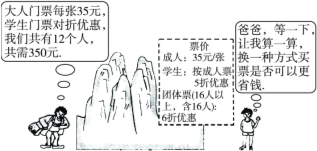
(1)小明他们一共去了几个成人?几个学生?
(2)请你帮小明算一算,用哪种方式买票更省钱?并说明理由.
-
科目: 来源: 题型:
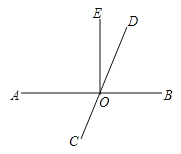
查看答案和解析>>【题目】如图,AB交CD于O,OE⊥AB.
(1)若∠EOD=20°,求∠AOC的度数;
(2)若∠AOC:∠BOC=1:2,求∠EOD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了60次实验,实验的结果如下:
(1)计算“3点朝上”的频率和“5点朝上”的频率;
(2)小颖说:“根据上述实验,一次实验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次”,小颖和小红的说法正确吗?为什么?
朝上的点数
1
2
3
4
5
6
出现的次数
7
9
6
8
20
10
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连结EF与边CD相交于点G,连结BE与对角线AC相交于点H,AE=CF,BE=EG.

(1)求证:EF∥AC;
(2)求∠BEF大小;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图案均是用长度相等的小木棒,按一定规律拼撘而成,第一个图案需4根小木棒,则第6个图案小木棒根数是( )
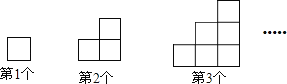
A.42 B.48 C.54 D.56
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x2﹣y2﹣3x﹣3y=__________.
相关试题

