【题目】庄子说:“一尺之椎,日取其半,万世不竭”.这句话(文字语言)表达了古人将事物无限分割的思想,用图形语言表示为图1,按此图分割的方法,可得到一个等式(符号语言):1=![]()
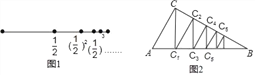
图2也是一种无限分割:在△ABC中,∠C=90°,∠B=30°,过点C作CC1⊥AB于点C1,再过点C1作C1C2⊥BC于点C2,又过点C2作C2C3⊥AB于点C3,如此无限继续下去,则可将利△ABC分割成△ACC1、△CC1C2、△C1C2C3、△C2C3C4、…、△Cn﹣2Cn﹣1Cn、….假设AC=2,这些三角形的面积和可以得到一个等式是_____.
参考答案:
【答案】2![]() =
=![]()
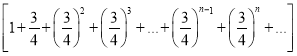
【解析】试题解析:如图2,∵AC=2,∠B=30°,CC1⊥AB,
∴Rt△ACC1中,∠ACC1=30°,且BC=2![]() ,
,
∴AC1=![]() AC=1,CC1=
AC=1,CC1=![]() AC1=
AC1=![]() ,
,
∴S△ACC1=![]() AC1CC1=
AC1CC1=![]() ×1×
×1×![]() =
=![]() ;
;
∵C1C2⊥BC,
∴∠CC1C2=∠ACC1=30°,
∴CC2=![]() CC1=
CC1=![]() ,C1C2=
,C1C2=![]() CC2=
CC2=![]() ,
,
∴![]() =
=![]() CC2C1C2=
CC2C1C2=![]() ×
×![]() ×
×![]() =
=![]() ×
×![]() ,
,
同理可得,
![]() =
=![]() ×(
×(![]() )2,
)2,
![]() =
=![]() ×(
×(![]() )3,
)3,
…
∴![]() =
=![]() ×(
×(![]() )n﹣1,
)n﹣1,
又∵S△ABC=![]() AC×BC=
AC×BC=![]() ×2×2
×2×2![]() =2
=2![]() ,
,
∴2![]() =
=![]() +
+![]() ×
×![]() +
+![]() ×(
×(![]() )2+
)2+![]() ×(
×(![]() )3+…+
)3+…+![]() ×(
×(![]() )n﹣1+…
)n﹣1+…
∴2![]() =
= .
.
故答案为:2![]() =
=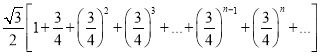 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程ax2+bx+c=0(a≠0)中,下列说法:
①若a+b+c=0,则b2﹣4ac>0;
②若方程两根为﹣1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
④若b=2a+c,则方程有两个不相等的实根.其中正确的有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
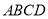 的边长为6,点
的边长为6,点 是
是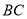 上的一点,连接
上的一点,连接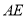 并延长交射线
并延长交射线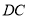 于点
于点 ,将
,将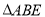 沿直线
沿直线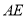 翻折,点
翻折,点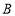 落在点
落在点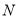 处,
处,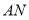 的延长线交
的延长线交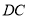 于点
于点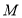 ,当
,当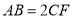 时,则
时,则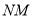 的长为________.
的长为________.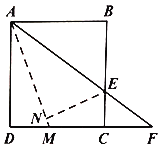
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,I是△ABC的内心,AI的延长线与△ABC的外接圆相交于点D,与BC交于点E,连接BI、CI、BD、DC.下列说法中正确的有( )
①∠CAD绕点A顺时针旋转一定的角度一定能与∠DAB重合;
②I到△ABC三个顶点的距离相等;③∠BIC=90°+
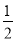 ∠BAC;
∠BAC;④线段DI是线段DE与DA的比例中项;⑤点D是△BIC的外心.
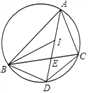
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.
(1)若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率;
(2)请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好全部配套组成GH型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?请列出二元一次方程组解答此问题.
(2)为了在规定期限内完成总任务,工厂决定补充一些新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置.1.设原来每天安排x名工人生产G型装置,后来补充m名新工人,求x的值(用含m的代数式表示)2.请问至少需要补充多少名新工人才能在规定期内完成总任务?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
我们给出如下定义:数轴上给定两点
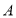 ,
,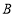 以及一条线段
以及一条线段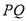 ,若线段
,若线段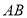 的中点
的中点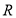 在线段
在线段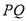 上(点
上(点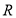 可以与点
可以与点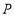 或
或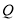 重合),则称点
重合),则称点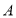 与点
与点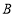 关于线段
关于线段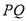 径向对称.下图为点
径向对称.下图为点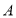 与点
与点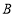 关于线段
关于线段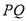 径向对称的示意图.
径向对称的示意图.
解答下列问题:
如图1,在数轴上,点
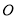 为原点,点
为原点,点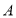 表示的数为-1,点
表示的数为-1,点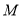 表示的数为2.
表示的数为2.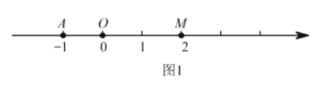
(1)①点
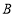 ,
,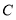 ,
,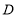 分别表示的数为-3,
分别表示的数为-3,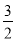 ,3,在
,3,在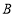 ,
,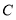 ,
,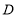 三点中, 与点
三点中, 与点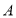 关于线段
关于线段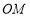 径向对称;
径向对称;②点
 表示的数为
表示的数为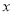 ,若点
,若点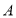 与点
与点 关于线段
关于线段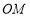 径向对称,则
径向对称,则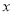 的取值范围是 ;
的取值范围是 ;(2)在数轴上,点
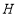 ,
,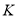 ,
,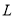 表示的数分别是-5,-4,-3,当点
表示的数分别是-5,-4,-3,当点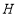 以每秒1个单位长度的速度向正半轴方向移动时,线段
以每秒1个单位长度的速度向正半轴方向移动时,线段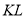 同时以每秒3个单位长度的速度向正半轴方向移动.设移动的时间为
同时以每秒3个单位长度的速度向正半轴方向移动.设移动的时间为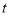 (
(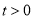 )秒,问
)秒,问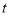 为何值时,线段
为何值时,线段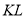 上至少存在一点与点
上至少存在一点与点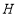 关于线段
关于线段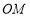 径向对称.
径向对称.
相关试题

