【题目】(方案设计题)某房地产集团筹建一小区,小区内居民楼南北朝向,楼高统一为16 m(共五层).已知该城市冬至日正午时分太阳高度最低,太阳光线与水平线的夹角为32°,所设计的南北两楼之间的距离为20 m(如图所示).

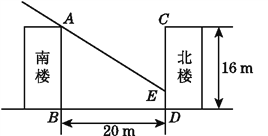
(1)试求出此时南楼的影子落在北楼上有多高;

(2)根据居住要求,每层居民在冬天都要有阳光,请你重新设计一下方案.(结果精确到0.1 m)

参考答案：

【答案】(1)南楼的影子落在北楼有约3.5 m高.

(2)重新设计时,两楼之间的距离至少应为25.6 m才能使每层居民在冬天都能得到阳光.

【解析】【试题分析】（1）利用tan ∠AEF= 得AF=EF·tan ∠AEF=20×tan 32°≈12.5(m)，再利用DE=BF=AB-AF≈16-12.5=3.5(m)即可；（2）根据tan 32°=，得BD==≈25.6(m)即可.

【试题解析】

(1)过E作EF⊥AB于F,

则BF=DE,EF=DB,∠AEF=32°.

在Rt△AEF中,∠AEF=32°,EF=20 m.

∵tan ∠AEF=,

∴AF=EF·tan ∠AEF=20×tan 32°≈12.5(m).

∴DE=BF=AB-AF≈16-12.5=3.5(m).

故南楼的影子落在北楼有约3.5 m高.

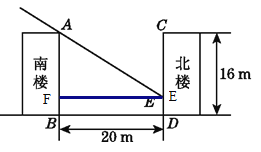
(2)若使每层居民在冬天都能得到阳光,则DE=0 m,即F与B重合,

∵tan ∠AEF=, 即tan 32°=,

∴BD==≈25.6(m).

故重新设计时,两楼之间的距离至少应为25.6 m才能使每层居民在冬天都能得到阳光.

关闭