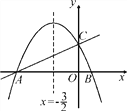
【题目】如图,在平面直角坐标系xOy中,直线y=![]() x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是直线x=-
x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是直线x=-![]() ,且经过A,C两点,与x轴的另一交点为点B.
,且经过A,C两点,与x轴的另一交点为点B.
(1)①直接写出点B的坐标;②求抛物线的解析式.
(2)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A,M,N为顶点的三角形与△ABC相似?若存在,求出点M的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)①点B的坐标为(1,0);②y=-![]() x2-
x2-![]() x+2;(2)存在点M1(0,2),M2(-3,2),M3(2,-3),M4(5,-18),使得以点A,M,N为顶点的三角形与△ABC相似.
x+2;(2)存在点M1(0,2),M2(-3,2),M3(2,-3),M4(5,-18),使得以点A,M,N为顶点的三角形与△ABC相似.
【解析】【试题分析】(1)①先求的直线y=![]() x+2与x轴、y轴交点的坐标,然后利用抛物线的对称性可求得点B的坐标;②设抛物线的解析式为y=y=a(x+4)(x﹣1),然后将点C的坐标代入即可求得a的值;(3)证明△ABC∽△ACO∽△CBO,然后分以下几种情况分类讨论即可:①当M点与C点重合,即M(0,2)时,△MAN∽△BAC;②根据抛物线的对称性,当M(﹣3,2)时,△MAN∽△ABC;③当点M在第四象限时,解题时,需要注意相似三角形的对应关系.
x+2与x轴、y轴交点的坐标,然后利用抛物线的对称性可求得点B的坐标;②设抛物线的解析式为y=y=a(x+4)(x﹣1),然后将点C的坐标代入即可求得a的值;(3)证明△ABC∽△ACO∽△CBO,然后分以下几种情况分类讨论即可:①当M点与C点重合,即M(0,2)时,△MAN∽△BAC;②根据抛物线的对称性,当M(﹣3,2)时,△MAN∽△ABC;③当点M在第四象限时,解题时,需要注意相似三角形的对应关系.
试题解析:
(1)①对于直线y=![]() x+2,当x=0时,y=2;当y=0时,x=-4,
x+2,当x=0时,y=2;当y=0时,x=-4,
∴C(0,2),A(-4,0),
由抛物线的对称性可知:点A与点B关于直线x=-![]() 对称,
对称,
∴点B的坐标为(1,0);
②∵抛物线y=ax2+bx+c过A(-4,0),B(1,0),
∴可设抛物线解析式为y=a(x+4)(x-1),
又∵抛物线过点C(0,2),
∴2=-4a,
∴a=-![]() ,
,
∴y=-![]() x2-
x2-![]() x+2
x+2
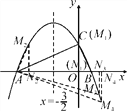
(2)在Rt△AOC中,易知△ABC∽△ACO∽△CBO,
如图,①当M点与C点重合,即M(0,2)时,△MAN∽△BAC;
②根据抛物线的对称性,当M(-3,2)时,△MAN∽△ABC;
③当点M在第四象限时,设M(n,-![]() n2-
n2-![]() n+2),则N(n,0),
n+2),则N(n,0),
∴MN=![]() n2+
n2+![]() n-2,AN=n+4,
n-2,AN=n+4,
当![]() =
=![]() 时,MN=
时,MN=![]() AN,即
AN,即![]() n2+
n2+![]() n-2=
n-2=![]() (n+4),
(n+4),
整理得n2+2n-8=0,解得n1=-4(舍),n2=2,
∴M(2,-3);
当![]() =
=![]() 时,MN=2AN,即
时,MN=2AN,即![]() n2+
n2+![]() n-2=2(n+4),
n-2=2(n+4),
整理得n2-n-20=0解得n1=-4(舍),n2=5,
∴M(5,-18).
综上所述,存在点M1(0,2),M2(-3,2),M3(2,-3),M4(5,-18),使得以点A,M,N为顶点的三角形与△ABC相似.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直角坐标系中,点P(1,4)在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的边BC与x轴重合,连接对角线BD交y轴于点E,过点A作AG⊥BD于点G,直线GF交AD于点F,AB、OC的长分别是一元二次方程x-5x+6=0的两根(AB>OC),且tan∠ADB=
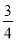 .
.(1)求点E、点G的坐标;
(2)直线GF分△AGD为△AGF与△DGF两个三角形,且S△AGF:S△DGF =3:1,求直线GF的解析式;
(3)点P在y轴上,在坐标平面内是否存在一点Q,使以点B、D、P、Q为顶点的四边形是矩形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
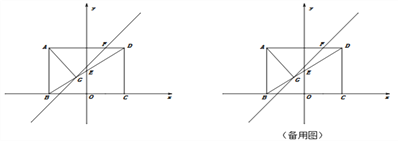
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程x2+3x+a=0有一个根为﹣1,则另一个根为( )
A.﹣2
B.2
C.4
D.﹣3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=68°,∠2=68°,∠3=112°.
(1)因为∠1=68°,∠2=68°(已知),
所以∠1=∠2.
所以_____________________∥_____________________ (同位角相等,两直线平行).
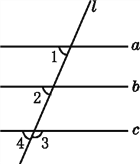
(2)因为∠3+∠4=180°(平角的定义),∠3=112°,
所以∠4=68°.
又因为∠2=68°,
所以∠2=∠4,
所以_________________∥_________________ (同位角相等,两直线平行).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线a,b,c,d,e,且∠1=∠2,∠3=∠4,则a与c平行吗?为什么?
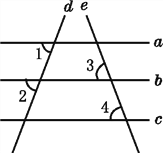
解:a与c平行.
理由:因为∠1=∠2(_________________),
所以a∥b(_________________).
因为∠3=∠4(_________________),
所以b∥c(_________________).
所以a∥c(_________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=2x+y,B=2x﹣y,计算A2﹣B2= .
相关试题

