搜索
【题目】如图,已知∠1=68°,∠2=68°,∠3=112°.
(1)因为∠1=68°,∠2=68°(已知),
所以∠1=∠2.
所以_____________________∥_____________________ (同位角相等,两直线平行).
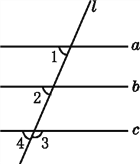
(2)因为∠3+∠4=180°(平角的定义),∠3=112°,
所以∠4=68°.
又因为∠2=68°,
所以∠2=∠4,
所以_________________∥_________________ (同位角相等,两直线平行).
参考答案：
【答案】(1)a;b (2)b;c
【解析】（1）求出∠1=∠2，根据平行线的判定推出：
∵∠1=68°，∠2=68°，
∴∠1=∠2，
∴直线a∥直线b，
故答案为：a，b；
（2）求出∠4的度数，求出∠2=∠4，根据平行线的判定推出：
∵∠3+∠4=180°，3=112°，
∴∠4=68°，
∵∠2=68°，
∴∠2=∠4，
∴直线b∥直线c，
故答案为：b，c．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD的边BC与x轴重合，连接对角线BD交y轴于点E，过点A作AG⊥BD于点G，直线GF交AD于点F，AB、OC的长分别是一元二次方程x-5x+6=0的两根（AB＞OC），且tan∠ADB=
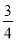.（1）求点E、点G的坐标；
（2）直线GF分△AGD为△AGF与△DGF两个三角形，且S△AGF：S△DGF =3:1，求直线GF的解析式；
（3）点P在y轴上，在坐标平面内是否存在一点Q，使以点B、D、P、Q为顶点的四边形是矩形？若存在，请直接写出点Q的坐标；若不存在，请说明理由.
-
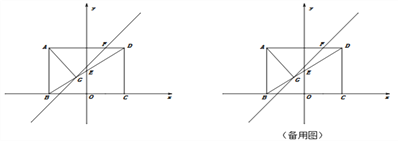
科目： 来源： 题型：
查看答案和解析>>【题目】若关于x的方程x2+3x+a=0有一个根为﹣1，则另一个根为（ ）
A.﹣2
B.2
C.4
D.﹣3 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，直线y＝
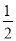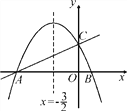
x＋2与x轴交于点A，与y轴交于点C.抛物线y＝ax2＋bx＋c的对称轴是直线x＝－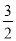
，且经过A，C两点，与x轴的另一交点为点B.(1)①直接写出点B的坐标；②求抛物线的解析式．
(2)抛物线上是否存在点M，过点M作MN垂直x轴于点N，使得以点A，M，N为顶点的三角形与△ABC相似？若存在，求出点M的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,已知直线a,b,c,d,e,且∠1=∠2,∠3=∠4,则a与c平行吗?为什么?
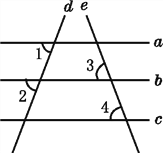
解:a与c平行.
理由:因为∠1=∠2(_________________),
所以a∥b(_________________).
因为∠3=∠4(_________________),
所以b∥c(_________________).
所以a∥c(_________________).
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知A=2x+y，B=2x﹣y，计算A2﹣B2= ．
-
科目： 来源： 题型：
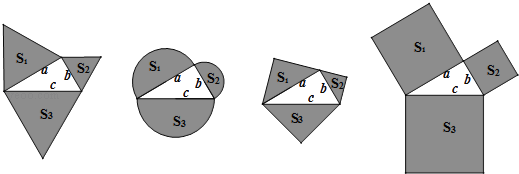
查看答案和解析>>【题目】如图，以直角三角形a、b、c为边，向外作等边三角形，半圆，等腰直角三角形和正方形，上述四种情况的面积关系满足S1+S2=S3图形个数有（ ）
A.1
B.2
C.3
D.4
相关试题
