【题目】如图,在正方形ABCD中,点E是对角线BD上任意一点,过点E作EF⊥BC于点F,作EG⊥CD于点G,若正方形ABCD的周长为a,则四边形EFCG的周长为_____.

参考答案:
【答案】![]()
【解析】
由ABCD为正方形,根据正方形的性质可知四条边相等,且∠CDB=∠CBD=45°,进而得到△DEG与△BEF都是等腰直角三角形,即EG与DG相等,EF与BF相等,由根据三个角为直角的四边形为矩形得到EFCG为矩形,从而得到对边EG与FC相等,EF与GC相等,故把四边形EFCG的周长转换为正方形的两条边相加,即为正方形周长的一半,由正方形的周长为a即可求出四边形EFCG的周长.
∵ABCD为正方形,
∴∠DBC=∠BDC=45°,AB=BC=CD=AD,
又∵EF⊥BC,EG⊥CD,
∴∠EFC=∠EGC=90°,又∠C=90°,
∴四边形EFCG为矩形,
∴EG=FC,EF=GC,
∵△BEF和△EDG都为等腰直角三角形,
∴DG=EG,EF=BF,
则四边形EFCG的周长=EF+FC+CG+EG
=DG+GC+CF+FB=DC+BC=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】旋转变换是解决数学问题中一种重要的思想方法,通过旋转变换可以将分散的条件集中到一起,从而方便解决问题.
已知,△ABC中,AB=AC,∠BAC=α,点D、E在边BC上,且∠DAE=
 α.
α.(1)如图1,当α=60°时,将△AEC绕点A顺时针旋转60°到△AFB的位置,连接DF,
①求∠DAF的度数;
②求证:△ADE≌△ADF;
(2)如图2,当α=90°时,猜想BD、DE、CE的数量关系,并说明理由;
(3)如图3,当α=120°,BD=4,CE=5时,请直接写出DE的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】点P是正方形ABCD边AB上一点(不与A,B重合),连接PD并将线段PD绕点P顺时针旋转90°,得线段PE,连接BE,则∠CBE等于( )

A. 75° B. 60° C. 45° D. 30°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, .
.⑴已知线段AB的垂直平分线与BC边交于点P,连结AP,求证:
 ;
;⑵以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q,连结AQ,若
 ,求
,求 的度数.
的度数.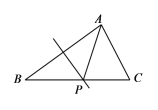

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15 km,CB=10 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小,此时∠MAN的度数为_________°.

-
科目: 来源: 题型:
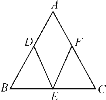
查看答案和解析>>【题目】如图,△ABC中,AB=AC,点D,E,F分别是△ABC边AB,BC,AC的中点,连接DE,EF,要使四边形ADEF是正方形,还需增加条件:_______.
相关试题

