【题目】如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15 km,CB=10 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?

参考答案:
【答案】收购站E应建在离A点10km处.
【解析】
根据使得C,D两村到E站的距离相等,需要证明DE=CE,再根据△DAE≌△EBC,得出AE=BC=10km;
∵使得C,D两村到E站的距离相等.
∴DE=CE,
∵DA⊥AB于A,CB⊥AB于B,
∴∠A=∠B=90°,
∴AE![]() +AD
+AD![]() =DE
=DE![]() ,BE
,BE![]() +BC
+BC![]() =EC
=EC![]() ,
,
∴AE![]() +AD
+AD![]() =BE
=BE![]() +BC
+BC![]() ,
,
设AE=x,则BE=ABAE=(25x),
∵DA=15km,CB=10km,
∴x![]() +15
+15![]() =(25x)
=(25x) ![]() +10
+10![]() ,
,
解得:x=10,
∴AE=10km,
∴收购站E应建在离A点10km处.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填在相应的括号内
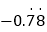 , -
, - , 0,
, 0, 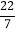 ,‐3.1415926, 20%, ‐3
,‐3.1415926, 20%, ‐3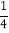 , 2, -1,3.1010010001…(每两个1之间逐次增加1个0)
, 2, -1,3.1010010001…(每两个1之间逐次增加1个0) ①正数集合{ ……}
②负数集合{ ……}
③整数集合{ ……}
④负分数集合{ ……}
⑤无理数集合{ ……}
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
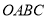 中,
中, 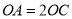 ,顶点
,顶点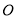 在坐标原点,顶点
在坐标原点,顶点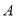 的坐标为(8,6).
的坐标为(8,6).(1)顶点
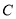 的坐标为( , ),顶点
的坐标为( , ),顶点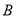 的坐标为( , );
的坐标为( , );(2)现有动点
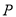 、
、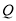 分别从
分别从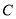 、
、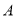 同时出发,点
同时出发,点 沿线段
沿线段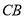 向终点
向终点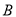 运动,速度为每秒2个单位,点
运动,速度为每秒2个单位,点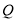 沿折线
沿折线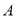 →
→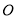 →
→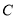 向终点
向终点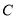 运动,速度为每秒
运动,速度为每秒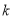 个单位.当运动时间为2秒时,以点
个单位.当运动时间为2秒时,以点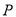 、
、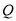 、
、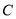 顶点的三角形是等腰三角形,求
顶点的三角形是等腰三角形,求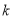 的值.
的值.(3)若矩形
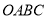 以每秒
以每秒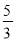 个单位的速度沿射线
个单位的速度沿射线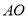 下滑,直至顶点
下滑,直至顶点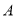 到达坐标原点时停止下滑.设矩形
到达坐标原点时停止下滑.设矩形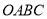 在
在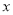 轴下方部分的面积为
轴下方部分的面积为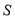 ,求
,求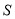 关于滑行时间
关于滑行时间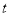 的函数关系式,并写出相应自变量
的函数关系式,并写出相应自变量 的取值范围.
的取值范围.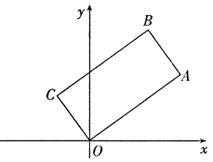
-
科目: 来源: 题型:
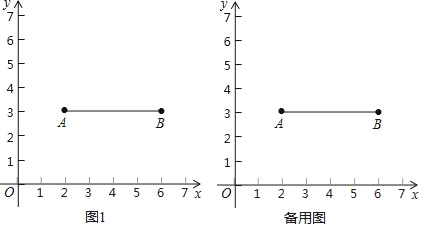
查看答案和解析>>【题目】如图,在平面直角坐标系中,给出如下定义:已知点A(2,3),点B(6,3),连接AB.如果线段AB上有一个点与点P的距离不大于1,那么称点P是线段AB的“环绕点”.
(1)已知点C(3,1.5),D(4,3.5),E(1,3),则是线段AB的“环绕点”的点是 ;
(2)已知点P(m,n)在反比例函数y=
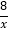 的图象上,且点P是线段AB的“环绕点”,求出点P的横坐标m的取值范围;
的图象上,且点P是线段AB的“环绕点”,求出点P的横坐标m的取值范围;(3)已知⊙M上有一点P是线段AB的“环绕点”,且点M(4,1),求⊙M的半径r的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过点A(2,0)的两条直线
 ,
, 分别交
分别交 轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=
轴于B,C,其中点B在原点上方,点C在原点下方,已知AB= .
.
(1)求点B的坐标;
(2)若△ABC的面积为4,求
 的解析式.
的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD的面积为300cm2,长和宽的比为3:2.在此长方形内沿着边的方向能否并排裁出两个面积均为147cm2的圆(π取3),请通过计算说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形ABC与三角形
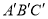 在平面直角坐标系中的位置如图所示,三角形
在平面直角坐标系中的位置如图所示,三角形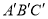 是由三角形ABC经过平移得到的.
是由三角形ABC经过平移得到的.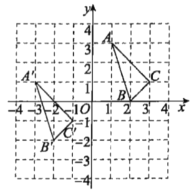
(1)分别写出点
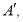
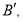
 的坐标;
的坐标;(2)说明三角形
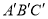 是由三角形ABC经过怎样的平移得到的;
是由三角形ABC经过怎样的平移得到的;(3)若点
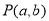 是三角形ABC内的一点,则平移后点P在三角形
是三角形ABC内的一点,则平移后点P在三角形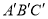 内的对应点为P‘,写出点P’的坐标.
内的对应点为P‘,写出点P’的坐标.
相关试题

