搜索
【题目】若2m=3，2n=2,则4m+2n=_____.
参考答案：
【答案】144
【解析】
直接利用幂的乘方运算法则将原式变形进而得出答案．
∵2m=3，2n=2，∴（2m）2=22m=9，24n=24=16，∴4m+2n =22m+4n =22m×24n=9×16=144．
故答案为：144．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果9－mx＋x2是一个完全平方式，则m的值为__________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列命题与其逆命题都是真命题的是（ ）
A. 全等三角形对应角相等 B. 对顶角相等
C. 角平分线上的点到角的两边的距离相等 D. 若a2>b2,则a>b
-
科目： 来源： 题型：
查看答案和解析>>【题目】(本题满分12分)如图1，为美化校园环境，某校计划在一块长为60米，宽为40米的长方形空地上修建一个长方形花圃，并将花圃四周余下的空地修建成同样宽的通道，设通道宽为
米.（1）花圃的面积为
（用含
的式子表示）；（2）如果通道所占面积是整个长方形空地面积的
，求出此时通道的宽；（3）已知某园林公司修建通道、花圃的造价
（元）、
（元）与修建面积
之间的函数关系如图2所示，如果学校决定由该公司承建此项目，并要求修建的通道的宽度不少于2米且不超过10米，那么通道宽为多少时，修建的通道和花圃的总造价为105920元 
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，
, 
.将△ABC绕点
顺时针旋转，得到△A1B1C.（1）如图1，当点
恰好在线段
的延长线上时，①求证：BB1∥CA1;
②求△AB1C的面积;
（2）如图2，点
是
上的中点，点
为线段
上的动点.在△ABC绕点
顺时针旋转过程中，点
的对应点是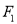
.求线段
长度的最大值与最小值的差.
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列计算正确的是（ ）
A. a2a3=a5 B. a2+a3=a5 C. （ab2）3=ab6 D. a10÷a2=a5
-
科目： 来源： 题型：
查看答案和解析>>【题目】先化简，再求值：3（2a﹣b）2﹣3a（4a﹣3b）+（2a+b）（2a﹣b）﹣b（a+b），其中a＝1，b＝2．
相关试题
