【题目】为了抓住文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不超过8 000元,那么该商店至多购进A种纪念品几件?
参考答案:
【答案】(1)A种纪念品每件100元,B种纪念品每件50元;
(2)商店至多可购进A种纪念品60件.
【解析】试题分析:(1)设A种纪念品每件需x元,B种纪念品每件需y元,根据条件建立方程组求出其解即可;
(2)设商店最多可购进A纪念品a件,则购进B纪念品件,根据购买这100件纪念品的资金不超过8000元为不相等关系建立不等式求出其解即可.
试题解析:(1)设A种纪念品每件需x元,B种纪念品每件需y元,
由题意,得![]() ,
,
解得: ![]() .
.
答:A种纪念品每件100元,B种纪念品每件50元;
(2)设商店可购进A纪念品a件,则购进B纪念品件,由题意得
100a+50≤8000,
解得:a≤60.
答:商店至多可购进A种纪念品60件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若多项式x2+mx+6因式分解的结果为(x-2)(x-3),则m=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋中装有20个球,其中7个黄球,8个黑球,5个红球,这些球只有颜色不同,其它都相同.
(1)求从袋中摸出一个球是黄球的概率;
(2)现从袋中取出若干个黑球,搅匀后,使从袋中摸出一个球是黑球的概率是 ,求从袋中取出黑球的个数.
,求从袋中取出黑球的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】将等腰直角△ABC斜放在平面直角坐标系中,使直角顶点C与点(1,0)重合,点A的坐标为(-2,1).
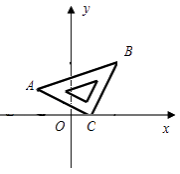
(1)求△ABC的面积S;
(2)求直线AB与y轴的交点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】a2m=2,b3n=3,求(b2n)3-a3mb3na5m的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O直径,BC为⊙O切线,连接A、C两点,交⊙O于点D,BE=CE,连接DE,OE.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=CD2OE;
(3)若cos∠BAD=
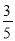 ,BE=6,求OE的长.
,BE=6,求OE的长.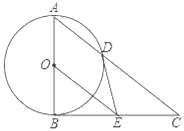
-
科目: 来源: 题型:
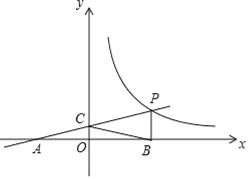
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数y=
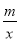 (x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.
(x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.(1)求一次函数,反比例函数的解析式;
(2)求证:点C为线段AP的中点;
(3)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,说明理由并求出点D的坐标;如果不存在,说明理由.
相关试题

