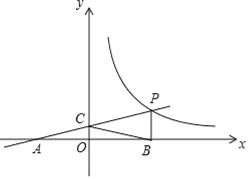
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() (x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.
(x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.
(1)求一次函数,反比例函数的解析式;
(2)求证:点C为线段AP的中点;
(3)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,说明理由并求出点D的坐标;如果不存在,说明理由.
参考答案:
【答案】(1)反比例函数解析式为y=![]() ,一次函数解析式为y=
,一次函数解析式为y=![]() x+1;
x+1;
(2)证明见解析;
(3)满足条件的点D,其坐标为(8,1).
【解析】试题分析:(1)由条件可求得P点坐标,利用待定系数法可求得一次函数和反比例函数的解析式;
(2)由平行线分线段成比例可求得AC=PC,可证得结论;
(3)可先求得C点坐标,过C作CD∥x轴,交PB于点E,交反比例函数图象于点D,可求得此时D点坐标,可证得四边形BCPD为菱形.
试题解析:(1)∵点A与点B关于y轴对称,
∴AO=BO,
∵A(﹣4,0),
∴B(4,0),
∵PB⊥x轴于点B,
∴P(4,2),
把P(4,2)代入反比例函数解析式可得m=8,
∴反比例函数解析式为y=![]() ,
,
把A、P两点坐标代入一次函数解析式可得![]() ,解得
,解得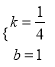 ,
,
∴一次函数解析式为y=![]() x+1;
x+1;
(2)证:∵点A与点B关于y轴对称,
∴OA=OB,
∵PB⊥x轴于点B,
∴∠PBA=∠COA=90°,
∴PB∥CO,
∴![]() =1,即AC=PC,
=1,即AC=PC,
∴点C为线段AP的中点;
(3)存在点D,使四边形BCPD为菱形.
理由如下:
∵点C为线段AP的中点,
∴BC=![]() AP=PC,
AP=PC,
∴BC和PC是菱形的两条边,
由y=![]() x+1可得C(0,1),
x+1可得C(0,1),
如图,过点C作CD∥x轴,交PB于点E,交反比例函数图象于点D,分别连接PD、BD,

∴D(8,1),且PB⊥CD,
∴PE=BE=1,CE=DE=4,
∴PB与CD互相垂直平分,即四边形BCPD为菱形,
∴存在满足条件的点D,其坐标为(8,1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了抓住文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不超过8 000元,那么该商店至多购进A种纪念品几件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】a2m=2,b3n=3,求(b2n)3-a3mb3na5m的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O直径,BC为⊙O切线,连接A、C两点,交⊙O于点D,BE=CE,连接DE,OE.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=CD2OE;
(3)若cos∠BAD=
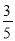 ,BE=6,求OE的长.
,BE=6,求OE的长.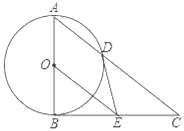
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数中,不可能成为一个三角形三边长的是( )
A. 3,5,9B. 4,9,9C. 6,8,10D. 7,3,8
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列现象:①电梯的升降运动;②飞机在地面上沿直线滑行;③风车的转动;④钟摆的摆动.其中属于平移的是( )
A. ①③B. ①②C. ②③D. ③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班有48人,在一次数学测验中,全班平均分为81分,已知不及格人数为6人,他们的平均分为46分,则及格学生的平均分是( )
A. 78分 B. 86分 C. 80分 D. 82分
相关试题

