搜索
【题目】两个连续奇数的平方差是（ ）
A.6的倍数
B.8的倍数
C.12的倍数
D.16的倍数
参考答案：
【答案】B
【解析】解：设两个连续奇数为2n+1，2n﹣1，
它们的平方差是（2n+1）2﹣（2n﹣1）2 ，
=（2n+1+2n﹣1）（2n+1﹣2n+1），
=4n2，
=8n，
故两个连续奇数的平方差是8的倍数．
故选B．
【考点精析】利用平方差公式对题目进行判断即可得到答案，需要熟知两数和乘两数差，等于两数平方差．积化和差变两项，完全平方不是它．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在数轴上表示数
， 
， 
， 
， 
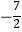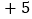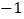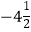。并把这些数用“＜”连接。 -
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两同学的家与学校的距离均为3000米．甲同学先步行600米，然后乘公交车去学校、乙同学骑自行车去学校．已知甲步行速度是乙骑自行车速度的
，公交车的速度是乙骑自行车速度的2倍．甲乙两同学同时从家发去学校，结果甲同学比乙同学早到2分钟．
（1）求乙骑自行车的速度；
（2）当甲到达学校时，乙同学离学校还有多远？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC和△DBC是两个具有公共边的全等三角形，AB=AC=3cm．BC=2cm，将△DBC沿射线BC平移一定的距离得到△D1B1C1，连接AC1，BD1．如果四边形ABD1C1是矩形，那么平移的距离为 cm．
-
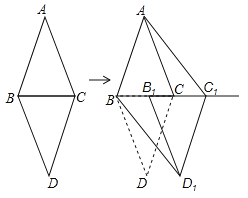
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面材料：
小伟遇到这样一个问题：如图1，在△ABC（其中∠BAC是一个可以变化的角）中，AB=2，AC=4，以BC为边在BC的下方作等边△PBC，求AP的最大值．
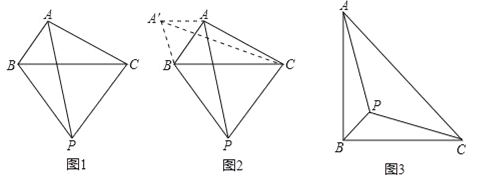
小伟是这样思考的：利用变换和等边三角形将边的位置重新组合．他的方法是以点B为旋转中心将△ABP逆时针旋转60°得到△A′BC，连接A′A，当点A落在A′C上时，此题可解（如图2）．
（1）请你回答：AP的最大值是 ．
（2）参考小伟同学思考问题的方法，解决下列问题：
如图3，等腰Rt△ABC．边AB=4，P为△ABC内部一点，请写出求AP+BP+CP的最小值长的解题思路．
提示：要解决AP+BP+CP的最小值问题，可仿照题目给出的做法．把△ABP绕B点逆时针旋转60，得到△A′BP′．
①请画出旋转后的图形
②请写出求AP+BP+CP的最小值的解题思路（结果可以不化简）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】△ABC在平面直角坐标系xOy中的位置如图所示．（不写解答过程，直接写出结果）
（1）若△A1B1C1与△ABC关于原点O成中心对称，则点A1的坐标为 ；
（2）将△ABC向右平移4个单位长度得到△A2B2C2，则点B2的坐标为 ；
（3）将△ABC绕O点顺时针方向旋转90°，则点C走过的路径长为 ；
（4）在x轴上找一点P，使PA+PB的值最小，则点P的坐标为 ．
-
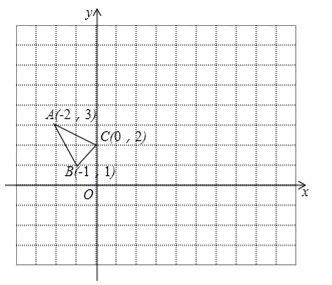
科目： 来源： 题型：
查看答案和解析>>【题目】下列命题中是真命题的有（ ）
①直径是圆中最大的弦；②长度相等的弧是等弧；③平分弦的直径垂直于弦，并且平分弦所对的两条弧；④两个圆心角相等，它们所对的弦也相等；⑤等弧所对的圆心角相等．
A.1个B.2个C.3个D.4个
相关试题
