【题目】甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去学校、乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的 ![]() ,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
(1)求乙骑自行车的速度;
(2)当甲到达学校时,乙同学离学校还有多远?
参考答案:
【答案】
(1)解:设乙骑自行车的速度为x米/分钟,则甲步行速度是 ![]() x米/分钟,公交车的速度是2x米/分钟,
x米/分钟,公交车的速度是2x米/分钟,
根据题意得 ![]() +
+ ![]() =
= ![]() ﹣2,
﹣2,
解得:x=300米/分钟,
经检验x=300是方程的根,
答:乙骑自行车的速度为300米/分钟
(2)解:∵300×2=600米,
答:当甲到达学校时,乙同学离学校还有600米
【解析】(1)设乙骑自行车的速度为x米/分钟,则甲步行速度是 ![]() x米/分钟,公交车的速度是2x米/分钟,根据题意列方程即可得到结论;(2)300×2=600米即可得到结果.
x米/分钟,公交车的速度是2x米/分钟,根据题意列方程即可得到结论;(2)300×2=600米即可得到结果.
-
科目: 来源: 题型:
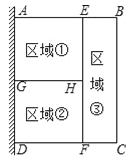
查看答案和解析>>【题目】如图,某小区准备用篱笆围成一块矩形花圃ABCD,为了节省篱笆,一边利用足够长的墙,另外三边用篱笆围着,再用两段篱笆EF与GH将矩形ABCD分割成①②③三块矩形区域,而且这三块矩形区域的面积相等,现有总长80m的篱笆,当围成的花圃ABCD的面积最大时,AB的长为 m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年春节期间,云南接待游客约2882万人,旅游收入约193亿元,其中2882万用科学记数法表示为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上表示数
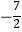 ,
, 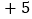 ,
, 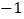 ,
, 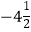 ,
, 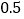 。并把这些数用“<”连接。
。并把这些数用“<”连接。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=3cm.BC=2cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1,连接AC1,BD1.如果四边形ABD1C1是矩形,那么平移的距离为 cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个连续奇数的平方差是( )
A.6的倍数
B.8的倍数
C.12的倍数
D.16的倍数 -
科目: 来源: 题型:
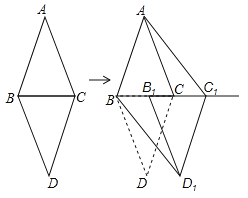
查看答案和解析>>【题目】阅读下面材料:
小伟遇到这样一个问题:如图1,在△ABC(其中∠BAC是一个可以变化的角)中,AB=2,AC=4,以BC为边在BC的下方作等边△PBC,求AP的最大值.
小伟是这样思考的:利用变换和等边三角形将边的位置重新组合.他的方法是以点B为旋转中心将△ABP逆时针旋转60°得到△A′BC,连接A′A,当点A落在A′C上时,此题可解(如图2).
(1)请你回答:AP的最大值是 .
(2)参考小伟同学思考问题的方法,解决下列问题:
如图3,等腰Rt△ABC.边AB=4,P为△ABC内部一点,请写出求AP+BP+CP的最小值长的解题思路.
提示:要解决AP+BP+CP的最小值问题,可仿照题目给出的做法.把△ABP绕B点逆时针旋转60,得到△A′BP′.
①请画出旋转后的图形
②请写出求AP+BP+CP的最小值的解题思路(结果可以不化简).
相关试题

