【题目】(1)如图,在□ABCD中,对角线AC、BD相交于点O.请找出图中的一对全等三角形,并给予证明;
(2)规定:一条弧所对的圆心角的度数作为这条弧的度数.
①如图,在⊙O中,弦AC、BD相交于点P,已知弧AB、弧CD分别为65°和45°,求∠APB;
②一般地,在⊙O中,弦AC、BD相交于点P,若弧AB、弧CD分别为m°和n°,求∠APB.
(用m、n的代数式表示)


参考答案:
【答案】(1)见解析;(2)①55°,②![]() (m°+n°).
(m°+n°).
【解析】【试题分析】
(1)答案不唯一,如:△AOB≌△COD.根据平行四边形的对角线相互平分,得AO=CO,OB=OD.因为对顶角相等,得∠AOB=∠COD,根据SAS,得:△AOB≌△COD.
(2)①如图:连接AD,

根据弧AB、弧CD分别为65°和45°,
根据同弧所对的圆周角等于圆心角的一半,得∠ADB=65°÷2=32.5°,∠CAD=45°÷2=22.5°,
根据三角形的外角等于与它不相邻的两个内角和,得,∠APB=32.5°+22.5°=55°.
②方法同①,得∠APB=![]() (m°+n°).
(m°+n°).
【试题解析】
(1)△AOB≌△COD.
∵四边形ABCD为平行四边形,
∴AO=CO,OB=OD.
∵∠AOB=∠COD,
∴△AOB≌△COD(SAS).
(2)①如图:连接AD,

∵弧AB、弧CD分别为65°和45°,
∴∠ADB=65°÷2=32.5°,
∠CAD=45°÷2=22.5°,
∴∠APB=32.5°+22.5°=55°.
②同理得∠APB=![]() (m°+n°).
(m°+n°).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,A(a,0),C(0,c)且满足:
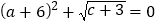 ,长方形ABCO在坐标系中(如图)点O为坐标系的原点。
,长方形ABCO在坐标系中(如图)点O为坐标系的原点。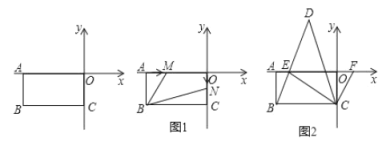
(1)求点B的坐标。
(2)如图1,若点M从点A出发,以2个单位/秒的速度向右运动(不超过点0),点N从原点O出发,以1个单位/秒的速度向下运动(不超过点C),设M、N两点同时出发,在它们运动的过程中,四边形MBNO的面积是否发生变化?若不变,求其值;若变化,求变化的范围。
(3)如图2,E为x轴负半轴上一点,且
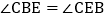 ,F是x轴正半轴上一动点,∠ECF的平分线CD交BE的延长线于点D,在点F运动的过程中,请探究∠CFE与∠D的数量关系并说明理由。
,F是x轴正半轴上一动点,∠ECF的平分线CD交BE的延长线于点D,在点F运动的过程中,请探究∠CFE与∠D的数量关系并说明理由。(注:三角形三个内角的和等于
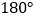 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件:_____________,使△AEH≌△CEB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)3x(x﹣1)=2﹣2x;
(2)
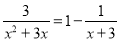 ;
;(3)先化简,后求值:(a2b)2(
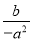 )3÷(﹣
)3÷(﹣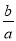 )4,其中a=(
)4,其中a=(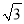 ﹣
﹣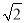 )0,b=(﹣
)0,b=(﹣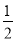 )﹣2.
)﹣2. -
科目: 来源: 题型:
查看答案和解析>>【题目】顺次连结一四边形各边的中点,若所得的四边形是一个菱形,则原四边形一定是( ).
A.矩形B.对角线相互垂直的四边形
C.平行四边形D.对角线相等的四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题.
 程大位,明代商人,珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).
程大位,明代商人,珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).在《算法统宗》里记载了一道趣题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完.试问大、小和尚各多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,下列条件中,不能说明AB⊥CD的是( )

A. ∠AOD=90°
B. ∠AOC=∠BOC
C. ∠BOC+∠BOD=180°
D. ∠AOC+∠BOD=180°
相关试题

