【题目】如图,点A1、A2、A3、…、An在抛物线y=x2图象上,点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn﹣1Bn都为等腰直角三角形(点B0是坐标原点),则△A2014B2013B2014的腰长等于( )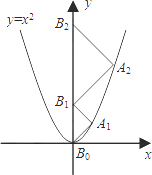
A.2013
B.2014
C.2013 ![]()
D.2014 ![]()
参考答案:
【答案】D
【解析】解:作A1C⊥y轴,A2E⊥y轴,垂足分别为C、E,
∵△A1B0B1、△A2B1B2都是等腰直角三角形,
∴B1C=B0C=DB0=A1D,B2E=B1E,
设A1(a,a),
将点A1的坐标代入解析式y=x2得:a=a2 ,
解得:a=0(不符合题意)或a=1,由勾股定理得:A1B0= ![]() ,
,
则B1B0=2,
过B1作B1N⊥A2F,设点A2(x2 , y2),
可得A2N=y2﹣2,B1N=x2=y2﹣2,
又点A2在抛物线上,所以y2=x22 , 即(x2+2)=x22 ,
解得x2=2,x2=﹣1(不合题意舍去),
则A2B1=2 ![]() ,同理可得:A3B2=3
,同理可得:A3B2=3 ![]() ,A4B3=4
,A4B3=4 ![]() …
…
∴A2014B2013=2014 ![]() ,
,
∴△A2014B2013B2014的腰长为:2014 ![]() .
.
故答案为:D.
利用等腰直角三角形的性质及点的坐标的关系求出第一个等腰直角三角形的腰长,用类似的方法求出第二个,第三个…的腰长,观察其规律,最后得出结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx的图象经过点(2,0)、(﹣1,6).

(1)求二次函数的解析式;
(2)画出它的图象;
(3)写出它的对称轴和顶点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2﹣2x+c的对称轴为直线x=﹣1,顶点为A,与y轴正半轴交点为B,且△ABO的面积为1.
(1)求抛物线的表达式;
(2)若点P在x轴上,且PA=PB,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标.
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出 A′、B′、C′的坐标,并在图中画出平移后图形.
(3)求出三角形ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如表是一个4×4(4行4列共16个“数”组成)的奇妙方阵,从这个方阵中选四个“数”,而且这四个“数”中的任何两个不在同一行,也不在同一列,有很多选法,把每次选出的四个“数”相加,其和是定值,则方阵中第三行三列的“数”是( )
30
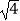
2
 sin60°
sin60°22
﹣3
﹣2
﹣
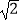 sin45°
sin45°0
|﹣5|
6
23
(
 )﹣1
)﹣14
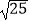
(
 )﹣1
)﹣1
A.5
B.6
C.7
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)填表,使上下每对x,y的值是方程3x+y=5的解
x
﹣2
0.4
y
0
3
(2)写出二元一次方程3x+y=5的正整数解: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知,
 满足
满足 点在
点在 轴的负半轴上,直角顶点
轴的负半轴上,直角顶点 在
在 轴上,点
轴上,点 在
在 轴上方.
轴上方.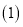 如图1所示,若点
如图1所示,若点 与原点重合,点
与原点重合,点 的坐标是
的坐标是 ,则点
,则点 的坐标是 ;
的坐标是 ;
 如图2所示,若点
如图2所示,若点 的坐标是
的坐标是 ,过点
,过点 作
作 轴于
轴于 ,请求出点
,请求出点 的坐标.
的坐标.
相关试题

