【题目】我校八年级学生去距学校15千米远的社会实践基地参加社会实践活动,一部分同学骑自行先走,过了40分钟后,其余同学乘汽车出发,结果他们同时到达.已知汽车的速度是骑车同学速度的3倍,求骑车同学的速度?
参考答案:
【答案】解:学生骑车速度为x千米/时,根据题意得:![]() .
.
解得:x=15,
经检验x=15是原分式方程的解,
答:骑车学生的速度是15千米/时.
【解析】求速度,路程已知,根据时间来列等量关系.关键描述语为:“一部分同学骑自行先走,过了40分钟后,其余同学乘汽车出发,结果他们同时到达”;等量关系为:骑自行车同学所用时间﹣乘车同学所用时间=![]() 小时,根据等量关系列出方程.
小时,根据等量关系列出方程.
【考点精析】利用分式方程的应用对题目进行判断即可得到答案,需要熟知列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位).
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算求值:
(1)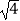 +
+ 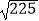 ﹣
﹣ 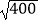
(2)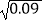 ﹣
﹣ 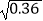
(3)|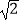 ﹣
﹣ 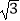 |+2
|+2 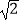
(4)3(x﹣1)3=﹣24. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AB的垂直平分线DE交AC于D,垂足为E,若∠A=30°,CD=3.
(1)求∠BDC的度数.
(2)求AC的长度.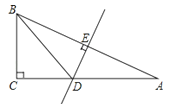
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,a//b,∠1=55°,∠2=40°,求∠3和∠4的度数.
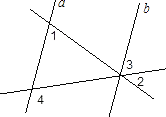
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)请写出图2中阴影部分的面积;
(2)观察图2你能写出下列三个代数式之间的等量关系吗?
代数式:(m+n)2 , (m﹣n)2 , mn;
(3)根据(2)中的等量关系,解决如下问题:若a+b=7,ab=5,求(a﹣b)2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1:已知△ABC中,以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE、CD,请你完成图形(尺规作图,不写作法.但要保留作图痕迹).
(2)如图2,已知△ABC中,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE、CD,判断BE与CD有什么数量关系,并加以证明.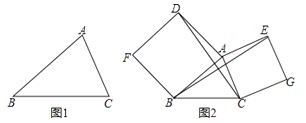
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB=90°,AC=BC,AD⊥MN于D,BE⊥MN于E;
(1)当直线MN绕点C旋转到图1的位置时,求证:
①△ADC≌△CEB;②DE=AD+BE.
(2)当直线MN绕点C旋转到图2的位置时,△ADC与△CEB还会全等吗?请直接回答会或不会;请直接猜想此时线段DE,AD,BE之间的数量关系,
相关试题

