【题目】如图, 直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() ,点
,点![]() 、
、![]() 分别为线段
分别为线段![]() 、
、![]() 的中点, 点
的中点, 点![]() 为
为![]() 上一动点, 当
上一动点, 当![]() 最小时, 点
最小时, 点![]() 的坐标为
的坐标为![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
参考答案:
【答案】C
【解析】
(方法一)根据一次函数解析式求出点A、B的坐标,再由中点坐标公式求出点C、D的坐标,根据对称的性质找出点D′的坐标,结合点C、D′的坐标求出直线CD′的解析式,令y=0即可求出x的值,从而得出点P的坐标.
(方法二)根据一次函数解析式求出点A、B的坐标,再由中点坐标公式求出点C、D的坐标,根据对称的性质找出点D′的坐标,根据三角形中位线定理即可得出点P为线段CD′的中点,由此即可得出点P的坐标.
解:(方法一)如图所示
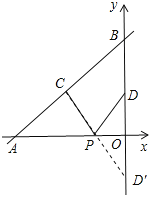
作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,
令y=![]() x+4中x=0,则y=4,
x+4中x=0,则y=4,
∴点B的坐标为(0,4);
令y=![]() x+4中y=0,则
x+4中y=0,则![]() x+4=0,解得:x=-6,
x+4=0,解得:x=-6,
∴点A的坐标为(-6,0).
∵点C、D分别为线段AB、OB的中点,
∴点C(-3,2),点D(0,2).
∵点D′和点D关于x轴对称,
∴点D′的坐标为(0,-2).
设直线CD′的解析式为y=kx+b,
∵直线CD′过点C(-3,2),D′(0,-2),
∴有![]() ,解得:
,解得: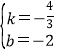 ,
,
∴直线CD′的解析式为y=![]() ,
,
令y=![]() 中y=0,则0=
中y=0,则0=![]() 解得:x=
解得:x=![]() ,
,
∴点P的坐标为![]() .
.
故选C.
(方法二)如图所示
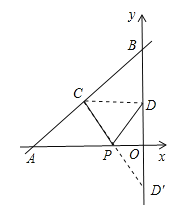
连接CD,作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,
令y=![]() 中x=0,则y=4,
中x=0,则y=4,
∴点B的坐标为(0,4);
令y=![]() 中y=0,则
中y=0,则![]() =0,解得:x=-6,
=0,解得:x=-6,
∴点A的坐标为(-6,0).
∵点C、D分别为线段AB、OB的中点,
∴点C(-3,2),点D(0,2),CD∥x轴,
∵点D′和点D关于x轴对称,
∴点D′的坐标为(0,-2),点O为线段DD′的中点.
又∵OP∥CD,
∴点P为线段CD′的中点,
∴点P的坐标为(![]() ).
).
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有
 筐白菜,以每筐
筐白菜,以每筐 千克为标准,超过或不足的分别用正、负来表示,记录如下:
千克为标准,超过或不足的分别用正、负来表示,记录如下:与标准质量的差
 单位:千克
单位:千克






筐 数




(1)与标准质量比较,
 筐白菜总计超过或不足多少千克?
筐白菜总计超过或不足多少千克?(2)若白菜每千克售价
 元,则出售这
元,则出售这 筐白菜可卖多少元?
筐白菜可卖多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,其对称轴为直线x=﹣1,给出下列结果:(1)b2>4ac;(2)abc>0;(3)2a+b=0;(4)a+b+c>0;(5)a﹣b+c<0.
则正确的结论是( )
A.(1)(2)(3)(4)
B.(2)(4)(5)
C.(2)(3)(4)
D.(1)(4)(5) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,随机地闭合开关S1 , S2 , S3 , S4 , S5中的三个,能够使灯泡L1 , L2同时发光的概率 .

-
科目: 来源: 题型:
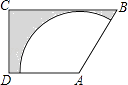
查看答案和解析>>【题目】如图,梯形ABCD中,AD∥BC,∠C=90°,AB=AD=4,BC=6,以点A为圆心在梯形内画出一个最大的扇形,则阴影部分的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知: 用 2 辆
 型车和 1 辆
型车和 1 辆 型车载满货物一次可运货 10 吨; 用 1 辆
型车载满货物一次可运货 10 吨; 用 1 辆 型车和 2 辆
型车和 2 辆 型车载满货物一次可运货 11 吨 . 根据以上信息, 解答下列问题:
型车载满货物一次可运货 11 吨 . 根据以上信息, 解答下列问题:(1) 1 辆
 型车和 1 辆
型车和 1 辆 型车载满货物一次可分别运货多少吨?
型车载满货物一次可分别运货多少吨?(2) 某物流公司现有货物若干吨要运输, 计划同时租用
 型车 6 辆,
型车 6 辆, 型车 8 辆, 一次运完, 且恰好每辆车都满载货物, 请求出该物流公司有多少吨货物要运输?
型车 8 辆, 一次运完, 且恰好每辆车都满载货物, 请求出该物流公司有多少吨货物要运输? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把抛物线y=
 x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=
x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=  x2交于点Q,则图中阴影部分的面积为 .
x2交于点Q,则图中阴影部分的面积为 . 
相关试题

