【题目】如图,在数学活动课中,小敏为了测量校园内旗杆CD的高度,先在教学楼的底端A点处,观测到旗杆顶端C的仰角∠CAD=60°,然后爬到教学楼上的B处,观测到旗杆底端D的俯角是30°,已知教学楼AB高4米.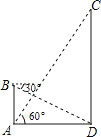
(1)求教学楼与旗杆的水平距离AD;(结果保留根号)
(2)求旗杆CD的高度.
参考答案:
【答案】
(1)
解:∵教学楼B点处观测到旗杆底端D的俯角是30°,
∴∠ADB=30°,
在Rt△ABD中,∠BAD=90°,∠ADB=30°,AB=4m,
∴AD= ![]() =
= ![]() =4
=4 ![]() (m),
(m),
答:教学楼与旗杆的水平距离是4 ![]() m.
m.
(2)
解:∵在Rt△ACD中,∠ADC=90°,∠CAD=60°,AD=4 ![]() m,
m,
∴CD=ADtan60°=4 ![]() ×
× ![]() =12(m),
=12(m),
答:旗杆CD的高度是12m.
【解析】(1)根据题意得出∠ADB=30°,进而利用锐角三角函数关系得出AD的长;
(2)利用(1)中所求,结合CD=ADtan60°求出答案.此题主要考查了解直角三角的应用,正确应用锐角三角函数关系是解题关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解茂名某水果批发市场荔枝的销售情况,某部门对该市场的三种荔枝品种A、B、C在6月上半月的销售进行调查统计,绘制成如下两个统计图(均不完整).请你结合图中的信息,解答下列问题:
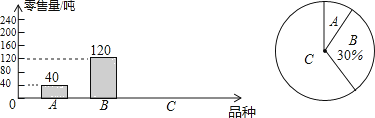
(1)该市场6月上半月共销售这三种荔枝多少吨?
(2)该市场某商场计划六月下半月进货A、B、C三种荔枝共500千克,根据该市场6月上半月的销售情况,求该商场应购进C品种荔枝多少千克比较合理? -
科目: 来源: 题型:
查看答案和解析>>【题目】有四张正面分别标有数字1,2,3,4的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗均匀.
(1)随机抽取一张卡片,求抽到数字“2”的概率;
(2)随机抽取一张卡片,然后不放回,再随机抽取一张卡片,请用列表或画树状图的方法求出第一次抽到数字“1”且第二次抽到数字“2”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB∥CD,∠ABE与∠CDE两个角的角平分线相交于点F.
(1)如图1,若∠E=80°,求∠BFD的度数.
(2)如图2,若∠ABM=
 ∠ABF,∠CDM=
∠ABF,∠CDM=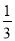 ∠CDF,试写出∠M与∠E之间的数量关系并证明你的结论.
∠CDF,试写出∠M与∠E之间的数量关系并证明你的结论.(3)若∠ABM=
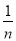 ∠ABF,∠CDM=
∠ABF,∠CDM=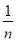 ∠CDF,∠E=m°,请直接用含有n,m°的代数式表示出∠M.
∠CDF,∠E=m°,请直接用含有n,m°的代数式表示出∠M.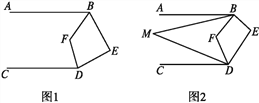
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABP与
 是两个全等的等边三角形,且
是两个全等的等边三角形,且 ,有下列四个结论:①
,有下列四个结论:① ,②
,② ,③
,③ ,④四边形ABCD是轴对称图形,其中正确的有
,④四边形ABCD是轴对称图形,其中正确的有
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是工人师傅用同一种材料制成的金属框架,已知
 ,
,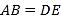 ,
, ,其中
,其中 的周长为24cm,
的周长为24cm, ,则制成整个金属框架所需这种材料的总长度为( )
,则制成整个金属框架所需这种材料的总长度为( )
A. 45cm B. 48cm C. 51cm D. 54cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用数轴解决问题:我们知道,若数轴上点
 表示的数是
表示的数是 ,点
,点 表示的数是
表示的数是 ,则
,则 、
、 两点间的距离记作
两点间的距离记作 ,
, .
.(1)若
 ,
, ,则
,则 = ;
= ; (2)若数轴上一点
 表示的数是
表示的数是 ,
, ,则
,则 = ;
= ;(3)若点
 表示的数是
表示的数是 ,已知
,已知 ,点
,点 在
在 的左边,
的左边, ,点
,点 在点
在点 的右边,
的右边, ,点
,点 以每秒
以每秒 的速度向右移动,同时点
的速度向右移动,同时点 、点
、点 分别以每秒
分别以每秒 、
、 的速度向左移动.设移动时间为
的速度向左移动.设移动时间为 秒,那么
秒,那么 是否有最小值?若有,求出最小值并写出此时
是否有最小值?若有,求出最小值并写出此时 的取值范围;若没有,请说明理由.
的取值范围;若没有,请说明理由.
相关试题

