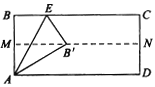
【题目】如图所示,将矩形ABCD纸对折,设折痕为MN,再把B点叠在折痕线MN上,(如图点B’),若![]() ,则折痕AE的长为( )
,则折痕AE的长为( )
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
参考答案:
【答案】C
【解析】
先作辅助线,然后根据折叠的性质和解直角三角形计算.
延长EB′与AD交于点F,
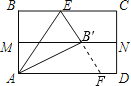
∵∠AB′E=∠B=90°,MN是对折折痕,
∴EB′=FB′,∠AB′E=∠AB′F,
在△AEB′和△AFB′中,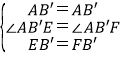 ,
,
∴△AEB′≌△AFB′,
∴AE=AF,
∴∠B′AE=∠B′AD(等腰三角形三线合一),
故根据题意,易得∠BAE=∠B′AE=∠B′AD;
故∠EAB=30°,
∴EB=![]() EA,
EA,
设EB=x,AE=2x,
∴(2x)2=x2+AB2,x=1,
∴AE=2,
则折痕AE=2,
故选:C.
-
科目: 来源: 题型:
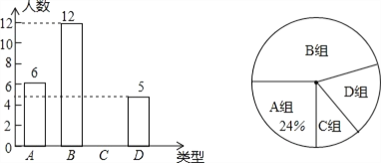
查看答案和解析>>【题目】为了解学生课余活动情况,某班对参加A组:绘画;B组:书法;C组:舞蹈;D组:乐器;这四个课外兴趣小组的人员分布情况进行抽样调查,并根据收集的数据绘制了如图两幅不完整的统计图,请根据图中提供信息,解答下面的问题:
(1)此次共调查了多少名同学?
(2)将条形统计图补充完整,
(3)计算扇形统计图中书法部分的圆心角的度数;
(4)已知在此次调查中,参加D组的5名学生中有3名女生和2名男生,要从这5名学生中随机抽取2名学生参加市举办的音乐赛,用列表法或画树状图的方法求出抽取的2名学生恰好是1男1女的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某校为了创建书香校园,去年购进一批图书.经了解,科普书的单价比文学书的单价多4元,用12000元购进的科普书与用8000元购进的文学书本数相等.
(1)文学书和科普书的单价各多少钱?
(2)今年文学书和科普书的单价和去年相比保持不变,该校打算用10000元再购进一批文学书和科普书,问购进文学书550本后至多还能购进多少本科普书?
-
科目: 来源: 题型:
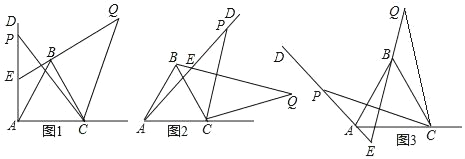
查看答案和解析>>【题目】如图1,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一点(点P与点A不重合),连结CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连结QB并延长交直线AD于点E.
(1)如图1,猜想∠QEP= °;
(2)如图2,3,若当∠DAC是锐角或钝角时,其它条件不变,猜想∠QEP的度数,选取一种情况加以证明;
(3)如图3,若∠DAC=135°,∠ACP=15°,且AC=4,求BQ的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】身高1.65米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形CDEF代表建筑物,兵兵位于建筑物前点B处,风筝挂在建筑物上方的树枝点G处(点G在FE的延长线上).经测量,兵兵与建筑物的距离BC=5米,建筑物底部宽FC=7米,风筝所在点G与建筑物顶点D及风筝线在手中的点A在同一条直线上,点A距地面的高度AB=1.4米,风筝线与水平线夹角为37°.
(1)求风筝距地面的高度GF;
(2)在建筑物后面有长5米的梯子MN,梯脚M在距墙3米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根米长的竹竿能否触到挂在树上的风筝?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

-
科目: 来源: 题型:
查看答案和解析>>【题目】山地自行车越来越受到中学生的喜爱,各种品牌相继投放市场,某车行经营的A型车去年销售总额为5万元,今年每辆销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
(1)今年A型车每辆售价多少元?(用列方程的方法解答)
(2)该车行计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A,B两种型号车的进货和销售价格如下表:
A型车
B型车
进货价格(元)
1100
1400
销售价格(元)
今年的销售价格
2000
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C的度数等于( )
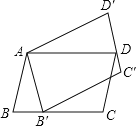
A. 100° B. 105° C. 115° D. 120°
相关试题

