【题目】为全面开展“阳光大课间”活动,某中学三个年级准备成立“足球”、“篮球”、“跳绳”、“踢毽”四个课外活动小组,学校体育组根据七年级学生的报名情况(每人限报一项)绘制了两幅不完整的统计图(如图), 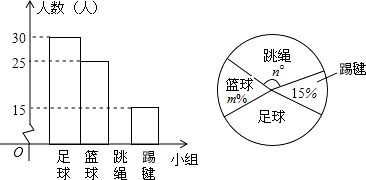
请根据以上信息,完成下列问题:
(1)m= , n= , 并将条形统计图补充完整;
(2)根据七年级的报名情况,试问全校2000人中,大约有多少人报名参加足球活动小组?
(3)根据活动需要,从“跳绳”小组的二男二女四名同学中随机选取两人到“踢毽”小组参加训练,请用列表或树状图的方法计算恰好选中一男一女两名同学的概率.
参考答案:
【答案】
(1)25;108
(2)解:2000× ![]() =600,
=600,
所以全校2000人中,大约有600人报名参加足球活动小组
(3)解:画树状图为:
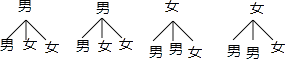
共有12种等可能的结果数,其中一男一女两名同学的结果数为8,
所以恰好选中一男一女两名同学的概率= ![]() =
= ![]()
【解析】解:(1)调查的总人数=15÷15%=100(人), 所以m%= ![]() ×100%=25%,即m=25,
×100%=25%,即m=25,
参加跳绳活动小组的人数=100﹣30﹣25﹣15=30(人),
所以n°= ![]() ×360°=108°,即n=108,
×360°=108°,即n=108,
如图,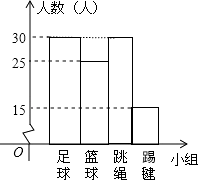
故答案为:25,108;
(1)先利用参加踢毽活动小组的人数它所占的百分比得到调查的总人数,再计算m的值和n的值,然后补全条形统计图;(2)利用样本估计总体,用2000乘以样本中参加足球活动小组的百分比即可;(3)画树状图展示所有12种等可能的结果数,再找出一男一女两名同学的结果数,然后根据概率公式求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,坐标平面上,二次函数y=﹣x2+4x﹣k的图形与x轴交于A,B两点,与y轴交于C点,其顶点为D,且k>0,若△ABC与△ABD的面积比为1:4,则k的值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值 (a﹣
 )(
)(  ﹣1)÷
﹣1)÷  ,其中a,b分别为关于x的一元二次方程x2﹣
,其中a,b分别为关于x的一元二次方程x2﹣ 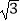 x+1=0的两个根.
x+1=0的两个根. -
科目: 来源: 题型:
查看答案和解析>>【题目】图①是小明在健身器材上进行仰卧起坐锻炼时的情景,图②是小明锻炼时上半身由ON位置运动到与地面垂直的OM位置时的示意图.已知AC=0.66米,BD=0.26米,α=20°.(参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)

(1)求AB的长(精确到0.01米);
(2)若测得ON=0.8米,试计算小明头顶由N点运动到M点的路径 的长度.(结果保留π)
的长度.(结果保留π) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF,连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.

(1)请判断:FG与CE的数量关系是 , 位置关系是;
(2)如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请出判断判断并给予证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.

(1)求证:DF是⊙O的切线;
(2)若DF=3,DE=2,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】正方形OABC的边长为4,对角线相交于点P,抛物线L经过O、P、A三点,点E是正方形内的抛物线上的动点.

(1)建立适当的平面直角坐标系,
①直接写出O、P、A三点坐标;
②求抛物线L的解析式;
(2)求△OAE与△OCE面积之和的最大值.
相关试题

