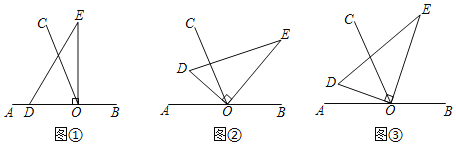
【题目】如图,以直线AB上一点O为端点作射线OC,使∠AOC=65°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图①,若直角三角板DOE的一边OD放在射线OA上,则∠COE= ;
(2)如图②,将直角三角板DOE绕点O顺时针方向转动到某个位置,若OC恰好平分∠AOE,求∠COD的度数;
(3)如图③,将直角三角板DOE绕点O任意转动,如果OD始终在∠AOC的内部,试猜想∠AOD和∠COE有怎样的数量关系?并说明理由.
参考答案:
【答案】(1)25° (2)25° (3)![]()
【解析】
(1)根据图形得出∠COE=∠DOE-∠AOC,代入求出即可;
(2)根据角平分线定义求出∠EOA=2∠AOC=130°,代入∠EOC=∠BOA-∠AOC,求出∠EOC,代入∠COD=∠DOE-∠EOC求出即可;
(3)根据图形得出∠AOD+∠COD=∠AOC=65°,∠COE+∠COD=∠DOE=90°,相减即可求出答案.
(1)如图①,∠COE=∠DOE-∠AOC=90°-65°=25°;
(2)如图②,∵OC平分∠EOA,∠AOC=65°,∴∠EOA=2∠AOC=130°,∵∠DOE=90°,∴∠AOD=∠AOE-∠DOE=40°,∵∠BOC=65°,∴∠COD=∠AOC-∠AOD=25°
(3)根据图形得出∠AOD+∠COD=∠AOC=65°,∠COE+∠COD=∠DOE=90°
∴![]()
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标平面内,直线y=﹣
 x﹣4与x轴、y轴分别交于点A、B,点C在x轴正半轴上,且满足OC=
x﹣4与x轴、y轴分别交于点A、B,点C在x轴正半轴上,且满足OC= OB.
OB.(1)求线段AB的长及点C的坐标;
(2)设线段BC的中点为E,如果梯形AECD的顶点D在y轴上,CE是底边,求点D的坐标和梯形AECD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=1,对角线AC、BD相交于点O,过点O作EF⊥AC分别交射线AD与射线CB于点E和点F,联结CE、AF.
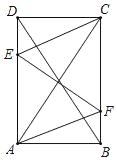
(1)求证:四边形AFCE是菱形;
(2)当点E、F分别在边AD和BC上时,如果设AD=x,菱形AFCE的面积是y,求y关于x的函数关系式,并写出x的取值范围;
(3)如果△ODE是等腰三角形,求AD的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于反比例函数
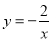 ,下列说法中不正确的是( )
,下列说法中不正确的是( )A. x>0时,y随x增大而增大
B. 图像分布在第二第四象限
C. 图像经过点(1.-2)
D. 若点A(
 )B(
)B( )在图像上,若
)在图像上,若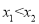 ,则
,则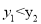
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下面给出的数轴中A表示1,B表示﹣2.5,回答下面的问题:
(1)A、B之间的距离是
(2)观察数轴,与点A的距离为5的点表示的数是: ;
(3)若将数轴折叠,使A点与﹣2表示的点重合,则B与数 表示的点重合
(4)若数轴上M、N两点之间的距离为2016(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:M: N: .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,M是BC的中点,且AM=9,BD=12,AD=10,则ABCD的面积是( )
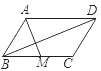
A. 30B. 36C. 54D. 72
-
科目: 来源: 题型:
查看答案和解析>>【题目】分别把下列各数填在所属的集合内:
+29,﹣3
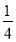 ,80%,﹣1,0.3,0,﹣31415,6,
,80%,﹣1,0.3,0,﹣31415,6,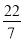
(1)正数集合:{_____…};
(2)负数集合:{_____…};
(3)整数集合:{_____…};
(4)分数集合:{_____…}.
相关试题

