【题目】观察下列等式:
1×2=![]() ×(1×2×3﹣0×1×2)
×(1×2×3﹣0×1×2)
2×3=![]() ×(2×3×4﹣1×2×3)
×(2×3×4﹣1×2×3)
3×4=![]() ×(3×4×5﹣2×3×4)
×(3×4×5﹣2×3×4)
…
计算:3×[1×2+2×3+3×4+…+n(n+1)]=_____.
参考答案:
【答案】n(n+1)(n+2)
【解析】试题解析:∵1×2=![]() ×(1×2×3-0×1×2)
×(1×2×3-0×1×2)
2×3=![]() ×(2×3×4-1×2×3),
×(2×3×4-1×2×3),
3×4=![]() ×(3×4×5-2×3×4),
×(3×4×5-2×3×4),
…,
∴n(n+1)=![]() [n(n+1)(n+2)-(n-1)n(n+1)],
[n(n+1)(n+2)-(n-1)n(n+1)],
∴3×[1×2+2×3+3×4+…+n(n+1)]
=3×![]() [1×2×3-0×1×2+2×3×4-1×2×3+3×4×5-2×3×4+…+n(n+1)(n+2)-(n-1)n(n+1)]
[1×2×3-0×1×2+2×3×4-1×2×3+3×4×5-2×3×4+…+n(n+1)(n+2)-(n-1)n(n+1)]
=n(n+1)(n+2).
故答案为:n(n+1)(n+2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】【发现证明】
如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.
【类比引申】
(1)如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;
【联想拓展】
(2)如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的边BC在x轴上,顶点A在y轴的正半轴上,OA=2,OB=1,OC=4.
(1)求过A、B、C三点的抛物线的解析式;
(2)设点M是x轴上的动点,试问:在平面直角坐标系中,是否存在点N,使得以点A,B,M,N为顶点的四边形是菱形?若存在,直接写出点N的坐标;若不存在,说明理由;
(3)若抛物线对称轴交x轴于点P,在平面直角坐标系中,是否存在点Q,使△PAQ是以PA为腰的等腰直角三角形?若存在,写出所有符合条件的点Q的坐标,选择一种情况加以说明;若不存在,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系中,函数y=mx+m和函数y=-mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A.
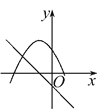 B.
B. 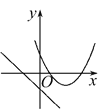 C.
C. 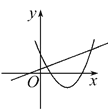 D.
D. 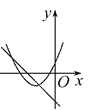
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(三角形顶点是网格线的交点)和△A1B1C1,且△ABC与△A1B1C1,成中心对称.
(1)画出△ABC和△A1B1C1的对称中心
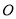 ;
;(2)将△A1B1C1沿直线
 方向向上平移6格,得到△A2B2C2,画出△A2B2C2;
方向向上平移6格,得到△A2B2C2,画出△A2B2C2;(3)将△A2B2C2绕点C2顺时针方向旋转90°,得到△A3B3C3,画出△A3B3C3.
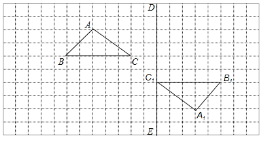
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平行四边形ABCD中,G为BC中点,点E在AD边上,且∠1=∠2.
(1)求证:E是AD中点;
(2)若F为CD延长线上一点,连接BF,且满足∠3=∠2,求证:CD=BF+DF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形。例如:某三角形三边长分别是5,6和8,因为
 ,所以这个三角形是常态三角形。
,所以这个三角形是常态三角形。(1)若△ABC三边长分别是2,
 和4,则此三角形_________常态三角形(填“是”或“不是”);
和4,则此三角形_________常态三角形(填“是”或“不是”);(2)若Rt△ABC是常态三角形,则此三角形的三边长之比为__________________(请按从小到大排列);
(3)如图,Rt△ABC中,∠ACB=90°,BC=6,点D为AB的中点,连接CD,若△BCD是常态三角形,求△ABC的面积。

相关试题

