【题目】我国宋朝数学家杨辉在他的著作![]() 详解九章算法
详解九章算法![]() 中提出“杨辉三角”
中提出“杨辉三角”![]() 如图
如图![]() ,此图揭示了
,此图揭示了![]() 为非负整数
为非负整数![]() 展开式的项数及各项系数的有关规律.
展开式的项数及各项系数的有关规律.
例如:![]() ,它只有一项,系数为1;系数和为1;
,它只有一项,系数为1;系数和为1;
![]() ,它有两项,系数分别为1,1,系数和为2;
,它有两项,系数分别为1,1,系数和为2;
![]() ,它有三项,系数分别为1,2,1,系数和为4;
,它有三项,系数分别为1,2,1,系数和为4;
![]() ,它有四项,系数分别为1,3,3,1,系数和为8;
,它有四项,系数分别为1,3,3,1,系数和为8;![]() ,
,
则![]() 的展开式共有______项,系数和为______.
的展开式共有______项,系数和为______.
参考答案:
【答案】![]()
![]()
【解析】
本题通过阅读理解寻找规律,观察可得(a+b)n(n为非负整数)展开式的各项系数的规律:首尾两项系数都是1,中间各项系数等于(a+b)n-1相邻两项的系数和.因此根据项数以及各项系数的和的变化规律,得出(a+b)n的项数以及各项系数的和即可.
根据规律可得,(a+b)n共有(n+1)项,
∵1=20
1+1=21
1+2+1=22
1+3+3+1=23
∴(a+b)n各项系数的和等于2n
故答案为:n+1,2n
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料后解决问题:
小明遇到下面一个问题:
计算(2+1)(22+1)(24+1)(28+1).
经过观察,小明发现如果将原式进行适当的变形后可以出现特殊的结构,进而可以应用平方差公式解决问题,具体解法如下:(2+1)(22+1)(24+1)(28+1)
=(2+1)(2﹣1)(22+1)(24+1)(28+1)
=(22﹣1)(22+1)(24+1)(28+1)
=(24﹣1)(24+1)(28+1)
=(28﹣1)(28+1)
=216﹣1
请你根据小明解决问题的方法,试着解决以下的问题:
(1)(2+1)(22+1)(24+1)(28+1)(216+1)=_____.
(2)(3+1)(32+1)(34+1)(38+1)(316+1)=_____.
(3)化简:(m+n)(m2+n2)(m4+n4)(m8+n8)(m16+n16).
-
科目: 来源: 题型:
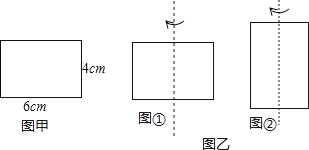
查看答案和解析>>【题目】探究:有一长6cm,宽4cm的矩形纸板,现要求以其一组对边中点所在直线为轴,旋转180°,得到一个圆柱,现可按照两种方案进行操作:
方案一:以较长的一组对边中点所在直线为轴旋转,如图①;
方案二:以较短的一组对边中点所在直线为轴旋转,如图②.
(1)请通过计算说明哪种方法构造的圆柱体积大;
(2)如果该矩形的长宽分别是5cm和3cm呢?请通过计算说明哪种方法构造的圆柱体积大;
(3)通过以上探究,你发现对于同一个矩形(不包括正方形),以其一组对边中点所在直线为轴旋转得到一个圆柱,怎样操作所得到的圆柱体积大(不必说明原因)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角三角形,两条直角边分别为6cm,8cm,斜边长为10cm,若分别以一边旋转一周(①结果用π表示;②你可能用到其中的一个公式,V圆柱=πr2h,V球体=
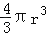 ,V圆锥=
,V圆锥=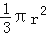 h)
h)(1)如果绕着它的斜边所在的直线旋转一周形成的几何体是?
(2)如果绕着它的直角边6所在的直线旋转一周形成的几何体的体积是多少?
(3)如果绕着它的斜边10所在的直线旋转一周形成的几何体的体积与绕着直角边8所在的直线旋转一周形成的几何体的体积哪个大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
 为等边三角形,
为等边三角形, ,
,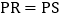 ,
,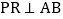 于R,
于R,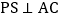 于S,则四个结论正确的是
于S,则四个结论正确的是

 点P在
点P在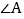 的平分线上;
的平分线上;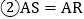 ;
;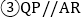 ;
;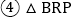 ≌
≌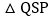 .
.
A. 全部正确 B. 仅
 和
和 正确 C. 仅
正确 C. 仅 正确 D. 仅
正确 D. 仅 和
和 正确
正确 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x+1与y轴交于A点,过点A的抛物线y=﹣
x+1与y轴交于A点,过点A的抛物线y=﹣  x2+bx+c与直线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).
x2+bx+c与直线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).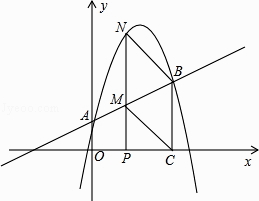
(1)直接写出抛物线的解析式;
(2)动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N,设点P移动的时间为t秒,MN的长度为s个单位,求s与t的函数关系式,并写出t的取值范围;
(3)设在(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?对于所求的t值,平行四边形BCMN是否菱形?请说明理由. -
科目: 来源: 题型:
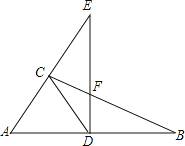
查看答案和解析>>【题目】如图,在
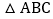 中,
中,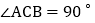 ,D是AB上的点,过点D作
,D是AB上的点,过点D作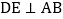 交BC于点F,交AC的延长线于点E,连接CD,
交BC于点F,交AC的延长线于点E,连接CD,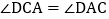 ,则下列结论正确的有______
,则下列结论正确的有______  将所有正确答案的序号都填在横线上
将所有正确答案的序号都填在横线上
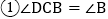 ;
;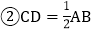 ;
;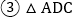 是等边三角形;
是等边三角形;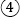 若
若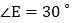 ,则
,则 .
.
相关试题

