搜索
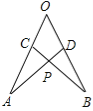
【题目】如图：在∠AOB的两边截取OA=OB，OC=OD，连接AD，BC交于点P，则下列结论中①△AOD≌△BOC，②△APC≌△BPD，③点P在∠AOB的平分线上。 正确的是 （填序号）
参考答案：
【答案】①②③
【解析】
试题分析：根据题中条件，由两边夹一角可得△AOD≌△BOC，得出对应角相等，又由已知得出AC=BD，可得△APC≌△BPD，同理连接OP，可证△AOP≌△BOP，进而可得出结论．
∵OA=OB，OC=OD，∠O为公共角，
∴△AOD≌△BOC，
∴∠A=∠B，
又∠APC=∠BPD，
∴∠ACP=∠BDP，
OA-OC=OB-OD，即AC=BD，
∴△APC≌△BPD，
∴AP=BP，
连接OP，
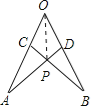
即可得△AOP≌△BOP，得出∠AOP=∠BOP，
∴点P在∠AOB的平分线上．
故题中结论都正确．
故答案为：①②③．
-
科目： 来源： 题型：
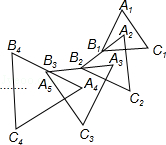
查看答案和解析>>【题目】如图，△A1B1C1是边长为1的等边三角形，A2为等边△A1B1C1的中心，连接A2B1并延长到点B2 ， 使A2B1=B1B2 ， 以A2B2为边作等边△A2B2C2 ， A3为等边△A2B2C2的中心，连接A3B2并延长到点B3 ， 使A3B2=B2B3 ， 以A3B3为边作等边△A3B3C3 ， 依次作下去得到等边△AnBnCn ， 则等边△A6B6C6的边长为 ．
-
科目： 来源： 题型：
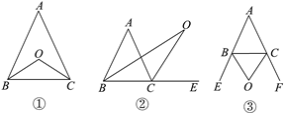
查看答案和解析>>【题目】探索三角形的内角与外角平分线(三角形的外角是三角形的一边与另一边的延长线所组成的角)：
(1)如图①，在△ABC中，BO平分∠ABC，CO平分∠ACB，若∠A＝50°，则∠BOC＝________；此时∠A与∠BOC有怎样的关系？试说明理由．
(2)如图②，BO平分∠ABC，CO平分∠ACE，若∠A＝50°，则∠BOC＝________；此时∠A与∠BOC有怎样的关系？试说明理由．
(3)如图③,△ABC的外角∠CBE,∠BCF的平分线BO，CO相交于点O，若∠A＝50°,则∠BOC＝______；此时∠A与∠BOC有怎样的关系？(不需说明理由)
-
科目： 来源： 题型：
查看答案和解析>>【题目】概念学习
规定：如果一个三角形的三个角分别等于另一个三角形的三个角，那么称这两个三角形互为“等角三角形”．
从三角形
不是等腰三角形
一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原来三角形是“等角三角形”，我们把这条线段叫做这个三角形的“等角分割线”．理解概念
如图1，在
中，
，
，请写出图中两对“等角三角形”
概念应用
如图2，在
中，CD为角平分线，
，
．求证：CD为
的等角分割线．
在中，
，CD是的等角分割线，直接写出
的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在长度为1个单位长度的小正方形组成的正方形中，点A、B、C在小正方形的顶点上．
在图中画出与
关于直线l成轴对称的
；
三角形ABC的面积为______；
以AC为边作与全等的三角形，则可作出______个三角形与全等；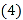
在直线l上找一点P，使
的长最短．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB边的垂直平分线
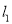交BC于D，AC边的垂直平分线
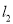交BC于E， 
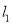与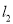
相交于点O，△ADE的周长为6cm．（1）求BC的长；
（2）分别连结OA、OB、OC，若△OBC的周长为16cm，求OA的长；
-
科目： 来源： 题型：
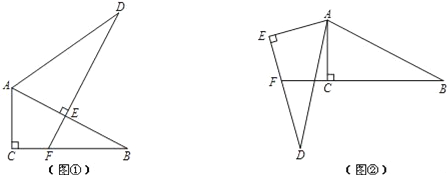
查看答案和解析>>【题目】已知Rt△ABC≌Rt△ADE，其中∠ACB=∠AED=90°．
（1）将这两个三角形按图①方式摆放，使点E落在AB上，DE的延长线交BC于点F．求证：BF+EF=DE；
（2）改变△ADE的位置，使DE交BC的延长线于点F（如图②），则（1）中的结论还成立吗？若成立，加以证明；若不成立，写出此时BF、EF与DE之间的等量关系，并说明理由．
相关试题
