【题目】邻边不相等的平行四边形纸片，剪去一个菱形，余下一个四边形，称为第一次操作；在余下的四边形纸片中再剪去一个菱形，又余下一个四边形，称为第二 次操作;……依此类推，若第n次操作余下的四边形是菱形，则称原平行四边形为n阶准菱形.如图1，平行四边形ABCD中，若AB=1，BC=2，则平行四 边形ABCD为1阶准菱形.

（I）判断与推理：

（i）邻边长分别为2和3的平行四边形是_________阶准菱形；

（ii）为了剪去一个菱形，进行如下操作：如图2，把平行四边形ABCD沿BE折叠（点E在AD上），使点A落在BC边上的点F，得到四边形ABFE，请证明四边形ABFE是菱形.

（Ⅱ）操作与计算：

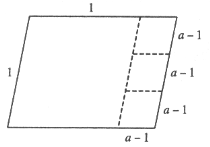
已知平行四边形ABCD的邻边长分别为l，a（a>1），且是3阶准菱形，请画出平行四边形ABCD及裁剪线的示意图，并在图形下方写出a的值.

参考答案：

【答案】

【解析】

试题分析：（1）①根据邻边长分别为2和3的平行四边形经过两次操作，即可得出所剩四边形是菱形，即可得出答案；

②根据平行四边形的性质得出AE∥BF，进而得出AE=BF，即可得出答案；

（2）①利用3阶准菱形的定义，即可得出答案；

②根据a=6b+r，b=5r，用r表示出各边长，进而利用图形得出ABCD是几阶准菱形．

试题解析：解：（I）（i）邻边长分别为2和3的平行四边形是2阶准菱形；

解：（I）（ii）如图2，由BE是四边形ABFE的对称轴，即知∠ABE=∠FBE，且AB=BF，EA=EF，又因为AE∥BF，所以∠AEB=∠FBE，从而有∠AEB=∠ABE，因此AB=AE，据此可知AB=AE=EF=BF，故四边形ABFE为菱形.

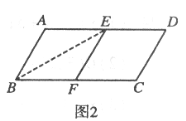
解：（II）①如图，必为a＞3,且a=4;

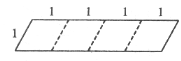
②如图，必为2<a<3，且a=2.5;

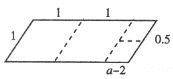
③如图，必为<a<2，且a-1+，解得a=;

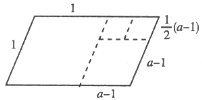
④如图，必为1<a<，且3（a-1）=1，解得a=.

综上所述，a的值分别是：a1=4，a2=，a3=，a4=.

关闭