【题目】已知二次函数y=x2+bx+c的图象过点A(﹣3,0)和点B(1,0),且与y轴交于点C,D点在抛物线上且横坐标是﹣2.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值.
参考答案:
【答案】
(1)
解:将A(﹣3,0),B(1,0)代入y=x2+bx+c,
得 ![]() ,
,
解得 ![]()
∴y=x2+2x﹣3
(2)
解:∵y=x2+2x﹣3=(x+1)2﹣4
∴对称轴x=﹣1,
又∵A,B关于对称轴对称,
∴连接BD与对称轴的交点即为所求P点.
过D作DF⊥x轴于F.将x=﹣2代入y=x2+2x﹣3,
则y=4﹣4﹣3=﹣3,
∴D(﹣2,﹣3)
∴DF=3,BF=1﹣(﹣2)=3
Rt△BDF中,BD= ![]()
∵PA=PB,
∴PA+PD=BD= ![]() .
.
故PA+PD的最小值为 ![]() .
.
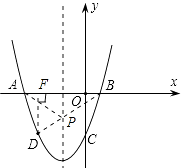
【解析】(1)把A(﹣3,0)和点B(1,0),代入y=x2+bx+c,建立关于b,c的二元一次方程组,求出b,c即可;(2)先求出抛物线的对称轴,又因为A,B关于对称轴对称,所以连接BD与对称轴的交点即为所求P点.
【考点精析】根据题目的已知条件,利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】一只不透明袋子中装有1个红球,2个黄球,这些球除颜色外都相同,小明搅匀后从中任意摸出一个球,记录颜色后放回、搅匀,再从中任意摸出1个球,用树状图或列表法列出摸出球的所有等可能情况,并求两次摸出的球都是黄色的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,E为CD上一点,F为BC延长线上一点,CE=CF.
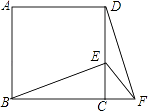
(1)△DCF可以看做是△BCE绕点C旋转某个角度得到的吗?说明理由.
(2)若∠CEB=60°,求∠EFD的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的中线,∠ADC=45°,把△ABC沿着直线AD对折,点C落在点E的位置,如果BC=12,那么线段BE的长度为( )

A.12
B.12
C.6
D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )

A.30°
B.45°
C.60°
D.75° -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣
 ,y2)、点C(
,y2)、点C(  ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2 , 且x1<x2 , 则x1<﹣1<5<x2 . 其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2 , 且x1<x2 , 则x1<﹣1<5<x2 . 其中正确的结论有( )
A.2个
B.3个
C.4个
D.5个
相关试题

