【题目】如图，正方形ABCD中，E为CD上一点，F为BC延长线上一点，CE=CF．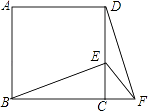
（1）△DCF可以看做是△BCE绕点C旋转某个角度得到的吗？说明理由．
（2）若∠CEB=60°，求∠EFD的度数．

参考答案：

【答案】
（1）证明：∵四边形ABCD是正方形，

∴DC=BC，∠DCB=∠FCE，

∵CE=CF，

∴△DCF≌△BCE，

则△DCF可以看作是△BCE绕点C顺时针旋转90°得到


（2）解：∵△BCE≌△DCF，

∴∠DFC=∠BEC=60°，

∵CE=CF，

∴∠CFE=45°，

∴∠EFD=15°


【解析】（1）根据正方形的性质及全等三角形的判定方法即可证明△BCE≌△DCF，据此即可解答；（2）由两个三角形全等的性质得出∠CFD的度数，再用等腰三角形的性质求∠EFD的度数．
【考点精析】利用正方形的性质和旋转的性质对题目进行判断即可得到答案，需要熟知正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形；①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了．

关闭