【题目】如图,AD是△ABC的中线,∠ADC=45°,把△ABC沿着直线AD对折,点C落在点E的位置,如果BC=12,那么线段BE的长度为( ) 
A.12
B.12 ![]()
C.6 ![]()
D.4 ![]()
参考答案:
【答案】C
【解析】解:根据折叠的性质知,CD=ED,∠CDA=∠ADE=45°, ∴∠CDE=∠BDE=90°,
∵AD是△ABC的中线
∴BD=CD,BC=12,
∴BD=ED=6,
即△EDB是等腰直角三角形,
∴BE= ![]() BD=
BD= ![]() ×6=6
×6=6 ![]() ,
,
故选C.
【考点精析】解答此题的关键在于理解翻折变换(折叠问题)的相关知识,掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一只不透明袋子中装有1个红球,2个黄球,这些球除颜色外都相同,小明搅匀后从中任意摸出一个球,记录颜色后放回、搅匀,再从中任意摸出1个球,用树状图或列表法列出摸出球的所有等可能情况,并求两次摸出的球都是黄色的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,E为CD上一点,F为BC延长线上一点,CE=CF.
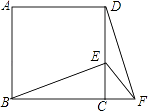
(1)△DCF可以看做是△BCE绕点C旋转某个角度得到的吗?说明理由.
(2)若∠CEB=60°,求∠EFD的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2+bx+c的图象过点A(﹣3,0)和点B(1,0),且与y轴交于点C,D点在抛物线上且横坐标是﹣2.

(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )

A.30°
B.45°
C.60°
D.75° -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣
 ,y2)、点C(
,y2)、点C(  ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2 , 且x1<x2 , 则x1<﹣1<5<x2 . 其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2 , 且x1<x2 , 则x1<﹣1<5<x2 . 其中正确的结论有( )
A.2个
B.3个
C.4个
D.5个 -
科目: 来源: 题型:
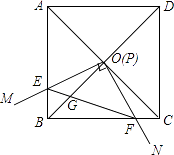
查看答案和解析>>【题目】如图,边长为1的正方形ABCD的对角线AC、BD相交于点O,有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是 .
(1)EF=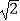 OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)BE+BF=
OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)BE+BF= 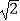 OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=  .
.
相关试题

