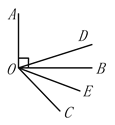
【题目】如图,DO平分∠AOC,OE平分∠BOC,若OA⊥OB,
(1)当∠BOC=30°,∠DOE=_______________; 当∠BOC=60°,∠DOE=_______________;
(2)通过上面的计算,猜想∠DOE的度数与∠AOB有什么关系,并说明理由.
参考答案:
【答案】 (1)45°, 45°;(2)∠DOE=![]() ∠AOB
∠AOB
【解析】试题分析:(1)先求出∠AOC,然后根据角平分线的定义求出∠COD和∠COE,最后根据∠DOE=∠COD-∠COE进行计算即可;
(2)设∠AOB=α,∠BOC=β,仿照(1)中的求出进行计算即可.
试题解析:
(1)①∵OA⊥OB,∠BOC=30°,
∴∠AOC=90°+30°=120°,
∵OD平分∠AOC,OE平分∠BOC,
∴∠COD=60°,∠COE=15°,
∴∠DOE=∠COD-∠COE=60°-15°=45°.
②∵OA⊥OB,∠BOC=60°,
∴∠AOC=90°+60°=150°,
∵OD平分∠AOC,OE平分∠BOC,
∴∠COD=75°,∠COE=30°,
∴∠DOE=∠COD-∠COE=75°-30°=45°.
(2)∠DOE=![]() ∠AOB.理由如下:
∠AOB.理由如下:
设∠AOB=α,∠BOC=β,
∵OD平分∠AOC,OE平分∠BOC,
∴∠COD=![]() (α+β),∠COE=
(α+β),∠COE=![]() β,
β,
∴∠DOE=∠COD-∠COE=![]() (α+β-β)=
(α+β-β)=![]() α=
α=![]() ∠AOB.
∠AOB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(-3x)3·(5x2y).
(2)
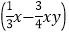 ·(-12y).
·(-12y).(3)(-4xy2)·
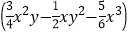 .
.(4)x3-2x
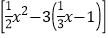 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线a 、b被直线c所截,现给出下列四种条件:
①∠2=∠6 ②∠2=∠8 ③∠1+∠4=180° ④∠3=∠8,其中能判断是a∥b的条件的序号是( )
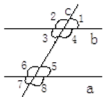
A. ①② B. ①③ C. ①④ D. ③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】同时掷两枚标有数字1~6的正方形骰子,数字和为1的概率是 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=2,BC=
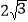 ,且∠BAC=120°,点D是线段BC上的一动点(不与点B、C重合),连接AD,作∠ADE=30°,DE交AC于点E.
,且∠BAC=120°,点D是线段BC上的一动点(不与点B、C重合),连接AD,作∠ADE=30°,DE交AC于点E.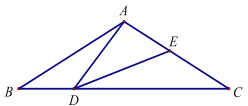
(1)求证:∠BAD∠EDC;
(2)当BD= 时,△ABD≌△EDC,并说明理由.
(3)当△ADE是直角三角形时,求AD的长?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一圆与平面直角坐标系中的x轴切于点A(8,0),与y轴交于点B(0,4),C(0,16),则该圆的直径为。

-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线
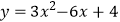 先向右平移3个单位长度,再向上平移2个单位长度后得到新的抛物线的顶点坐标为 .
先向右平移3个单位长度,再向上平移2个单位长度后得到新的抛物线的顶点坐标为 .
相关试题

