【题目】已知Rt△ABC中,∠C=90°,AC=BC,直线m经过点C,分别过点A,B作直线m的垂线,垂足分别为点E,F,若AE=3,AC=5,则线段EF的长为_______.
参考答案:
【答案】1或7
【解析】分两种情况:①如图1所示:先证出∠1=∠3,由勾股定理求出CE,再证明△BCF≌△CAE,得出对应边相等CF=AE=3,得出EF=CE-CF即可;
②如图2所示:先证出∠1=∠3,由勾股定理求出CE,再证明△BCF≌△CAE,得出对应边相等CF=AE=3,得出EF=CE+CF即可.
分两种情况:①如图1所示:
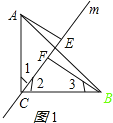
∵∠ACB=90°,
∴∠1+∠2=90°,
∵BF⊥m,
∴∠BFC=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
∵AE⊥m,
∴∠AEC=90°,
∴CE=![]() =4,
=4,
在△BCF和△CAE中,
 ,
,
∴△BCF≌△CAE(AAS),
∴CF=AE=3,
∴EF=CE-CF=4-3=1;
②如图2所示:

∵∠ACB=90°,
∴∠1+∠2=90°,
∵BF⊥m,
∴∠BFC=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
∵AE⊥m,
∴∠AEC=90°,
∴CE=![]() =4,
=4,
在△BCF和△CAE中,
 ,
,
∴△BCF≌△CAE(AAS),
∴CF=AE=3,
∴EF=CE+CF=4+3=7;
综上所述:线段EF的长为:1或7.
故答案为:1或7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内有一点D,且DA=DB=DC.若∠DAB=20°,∠DAC=30°,则∠BDC的度数为( )

A. 100° B. 80° C. 70° D. 50°
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
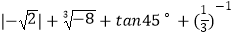 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于点E,交AC于点F,过点O作OD⊥AC于点D,下列四个结论:
①EF=BE+CF;
②∠BOC=90°+
 ∠A;
∠A;③点O到△ABC各边的距离相等;
④设OD=m,AE+AF=n,则S△AEF=mn.
其中正确的结论是( )
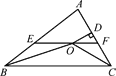
A. ①②③ B. ①②④ C. ②③④ D. ①③④
-
科目: 来源: 题型:
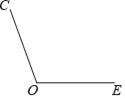
查看答案和解析>>【题目】已知∠EOC=110°,将角的一边OE绕点O旋转,使终止位置OD和起始位置OE成一条直线,以点O为中心将OC顺时针旋转到OA,使∠COA=∠DOC,过点O作∠COA的平分线OB.
(1)借助量角器、直尺补全图形;
(2)求∠BOE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点C是线段AB上的一点,点D是线段AB的中点,点E是线段BC的中点.
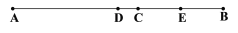
(1)当AC=10,BC=8时,求线段DE的长度;
(2)当AC=m,BC=n(m>n)时,求线段DE的长度;
(3)从(1)(2)的结果中,你发现了什么规律?请直接写出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小慧两位同学在数学活动课中,把长为30cm,宽为10cm的长方形白纸条粘合起来,小明按如图甲所示的方法粘合起来得到长方形ABCD,粘合部分的长度为6cm,小慧按如图乙所示的方法粘合起来得到长方形A1B1C1D1,黏合部分的长度为4cm.若长为30cm,宽为10cm的长方形白纸条共有100张,则小明应分配到 张长方形白纸条,才能使小明和小慧按各自要求黏合起来的长方形面积相等(要求100张长方形白纸条全部用完).

相关试题

