搜索
【题目】如图，在四边形
中，
是
边的中点，连接
并延长交
的延长线于点
，且
添加一个条件使四边形是平行四边形，下面四个条件中可选择的是（ ）
A.
B.
C.
D.
参考答案：
【答案】D
【解析】
把A、B、C、D四个选项中的条件分别代入验证，发现D为正确选项，添加
时，可先证明△AED≌△BEF，得到AD＝BF＝CB，结合AD∥FC可得四边形
是平行四边形．
解：A. 添加
时，无法证明AB∥CD或AD＝BC，故不能使四边形是平行四边形，不合题意；
B. 添加
时，无法证明AD∥BC或AB＝CD，故不能使四边形是平行四边形，不合题意；
C. 添加
时，无法证明∠ABC＝∠ADC，故不能使四边形是平行四边形，不合题意；
D. ∵，
∴AD∥FC，
在△AED和△BEF中，
，
∴△AED≌△BEF（AAS），
∴AD＝BF，
∵
，
∴AD＝CB，
∴四边形是平行四边形，符合题意；
故选：D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
中，
，
，
，若动点P从点C开始，按
的路径运动，且速度为每秒1cm，设出发的时间为t秒．
出发2秒后，求
的面积；
当t为几秒时，BP平分
；
问t为何值时，
为等腰三角形？ -
科目： 来源： 题型：
查看答案和解析>>【题目】某校为学生开展拓展性课程，拟在一块长比宽多6米的长方形场地内建造由两个大棚组成的植物养殖区（如图1），要求两个大棚之间有间隔4米的路，设计方案如图2，已知每个大棚的周长为44米．
（1）求每个大棚的长和宽各是多少？
（2）现有两种大棚造价的方案，方案一是每平方米60元，超过100平方米优惠500元，方案二是每平方米70元，超过100平方米优惠总价的20%，试问选择哪种方案更优惠？
-
科目： 来源： 题型：
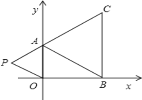
查看答案和解析>>【题目】如图，在下面直角坐标系中，已知A（0，a），B（b，0），C（b，c）三点，其中a、b、c满足关系式
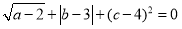．（1）求a、b、c的值；
（2）如果在第二象限内有一点P（m，
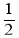），请用含m的式子表示四边形ABOP的面积；（3）在（2）的条件下，是否存在点P，使四边形ABOP的面积与△ABC的面积相等？若存在，求出点P的坐标，若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，G是线段AB上一点，AC和DG相交于点E．
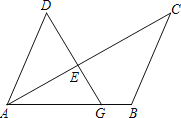
（1）请先作出∠ABC的平分线BF，交AC于点F；（尺规作图，保留作图痕迹，不写作法与证明）
（2）然后证明当：AD∥BC，AD＝BC，∠ABC＝2∠ADG时，DE＝BF．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知在
中，对角线
，
，
平分
交
的延长线于点
，连接
．（1）求证：
．（2）设
，连接
交
于点
．画出图形，并求的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某石化乙烯厂某车间生产甲、乙两种塑料的相关信息如下表，请你解答下列问题：
出厂价
成本价
排污处理费
甲种塑料
2100（元/吨）
800（元/吨）
200（元/吨）
乙种塑料
2400（元/吨）
1100（元/吨）
100（元/吨）
另每月还需支付设备管理、维护费20000元
（1）设该车间每月生产甲、乙两种塑料各x吨，利润分别为y1元和y2元，分别求出y1和y2与x的函数关系式(注：利润=总收入-总支出)；
（2）已知该车间每月生产甲、乙两种塑料均不超过400吨，若某月要生产甲、乙两种塑料共700吨，求该月生产甲、乙塑料各多少吨时，获得的总利润最大？最大利润是多少？
相关试题
