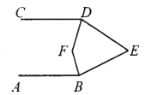
【题目】如图,![]() ,
,![]() ,
,![]() 的平分线与
的平分线与![]() 的平分线交于点
的平分线交于点![]() ,则
,则![]() 的度数是________.
的度数是________.
参考答案:
【答案】![]()
【解析】
过点E作EG∥AB,过点F作FP∥AB,根据平行线的性质可得∠ABE+∠BEG=180°,∠GED+∠EDC=180°,根据角的计算以及角平分线的定义可得∠FBE+∠EDF=![]() (∠ABE+∠CDE),再依据∠ABF=∠BFP,∠CDF=∠DFP结合角的计算即可得出结论.
(∠ABE+∠CDE),再依据∠ABF=∠BFP,∠CDF=∠DFP结合角的计算即可得出结论.
解:如图,过点E作EG∥AB,过点F作FP∥AB,
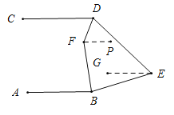
∵AB∥CD,
∴AB∥CD∥GE∥FP
∴∠ABE+∠BEG=180°,∠GED+∠EDC=180°,
∴∠ABE+∠CDE+∠BED=360°;
又∵∠BED=60°,
∴∠ABE+∠CDE=300°.
∵∠ABE和∠CDE的平分线相交于F,
∴∠ABF+∠CDF=![]() (∠ABE+∠CDE)=150°,
(∠ABE+∠CDE)=150°,
∵FP∥AB,AB∥CD,
∴AB∥CD∥FP,
∴∠ABF=∠BFP,∠CDF=∠DFP
∴∠BFD=∠BFP+∠DFP=∠ABF+∠CDF =150°.
故答案为:150°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一名考生步行前往考场,5分钟走了总路程的
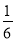 ,估计步行不能准时到达,于是他改乘出租车赶往考场,他的行程与时间关系如图所示(假定总路程为1,出租车匀速),则他到达考场所花的时间比一直步行提前了________分钟。
,估计步行不能准时到达,于是他改乘出租车赶往考场,他的行程与时间关系如图所示(假定总路程为1,出租车匀速),则他到达考场所花的时间比一直步行提前了________分钟。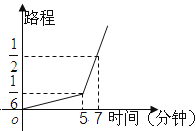
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,己知抛物线
 与直线
与直线 的一个交点记为A,点A的横坐标是-3.
的一个交点记为A,点A的横坐标是-3.
(1)求抛物线M1的表达式及它的顶点坐标;
(2)将抛物线
 向右平移3个单位,再向上平移3个单位,得到抛物线M2,直线
向右平移3个单位,再向上平移3个单位,得到抛物线M2,直线 与M2的一个交点记为B,点C是线段AB上的一个动点,过点C作x轴的垂线,垂足为D,在CD的右侧作正方形CDEF.
与M2的一个交点记为B,点C是线段AB上的一个动点,过点C作x轴的垂线,垂足为D,在CD的右侧作正方形CDEF.①当点C的横坐标为2时,直线y=x+n恰好经过正方形CDEF的顶点F,求此时n的值;
②在点C的运动过程中,若直线y=x+n与正方形CDEF始终没有公共点,求n的取值范围(直接写出结果).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上,已知点
 ,
, 分别表示数1,
分别表示数1, ,那么数轴上表示数
,那么数轴上表示数 的点应落在( )
的点应落在( )
A.点
 的左边B.线段
的左边B.线段 上C.点
上C.点 的右边D.数轴的任意位置
的右边D.数轴的任意位置 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线
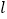 平行于直线EC,且直线
平行于直线EC,且直线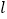 与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线
与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线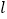 上, 则DF的长为_____
上, 则DF的长为_____
-
科目: 来源: 题型:
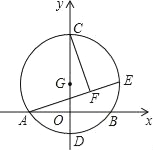
查看答案和解析>>【题目】如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )
A.
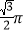 B.
B. 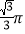 C.
C. 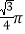 D.
D. 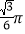
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程组解应用题
5月份,甲、乙两个工厂用水量共为200吨.进入夏季用水高峰期后,两工厂积极响应国家号召,采取节水措施.6月份,甲工厂用水量比5月份减少了15%,乙工厂用水量比5月份减少了10%,两个工厂6月份用水量共为174吨,求两个工厂5月份的用水量各是多少?
相关试题

