【题目】如图,己知抛物线![]() 与直线
与直线![]() 的一个交点记为A,点A的横坐标是-3.
的一个交点记为A,点A的横坐标是-3.

(1)求抛物线M1的表达式及它的顶点坐标;
(2)将抛物线![]() 向右平移3个单位,再向上平移3个单位,得到抛物线M2,直线
向右平移3个单位,再向上平移3个单位,得到抛物线M2,直线![]() 与M2的一个交点记为B,点C是线段AB上的一个动点,过点C作x轴的垂线,垂足为D,在CD的右侧作正方形CDEF.
与M2的一个交点记为B,点C是线段AB上的一个动点,过点C作x轴的垂线,垂足为D,在CD的右侧作正方形CDEF.
①当点C的横坐标为2时,直线y=x+n恰好经过正方形CDEF的顶点F,求此时n的值;
②在点C的运动过程中,若直线y=x+n与正方形CDEF始终没有公共点,求n的取值范围(直接写出结果).
参考答案:
【答案】(1)![]() ,顶点为
,顶点为![]() ;(2)①
;(2)①![]() ,②
,②![]()
【解析】分析:(1)将点A横坐标代入y=x,即可得出点A纵坐标,从而得出点A的坐标,根据点A在抛物线M1:y=ax2+4x上,代入即可得出a的值,将抛物线M1化为顶点式,根据平移的原则即可得出抛物线M2;
(2)①把点C横坐标代入y=x,即可得出点C坐标,从而得出点F坐标,把点F代入y=x+n即可得出n的值;
②根据直线y=x+n与正方形CDEF始终没有公共点,直接可得出n的取值范围.
详解:(1)∵点A在直线y=x,且点A的横坐标是-3,
∴A(-3,-3),
把A(-3,-3)代入y=ax2+4x,
解得a=1.
∴M1:y=x2+4x,顶点为(-2,-4).
∴M2的顶点为(1,-1).
∴M2的表达式为y=x2-2x.
(2)①由题意,C(2,2),
∴F(4,2).
∵直线y=x+n经过点F,
∴2=4+n.
解得n=-2.
②由题意得:n的取值范围是n>3,n<-6.

-
科目: 来源: 题型:
查看答案和解析>>【题目】高新一中初中校区名校+教育联合体主题美术展在西安高新区都市之门举办,学校组织七年级部分学生乘车参观展览,若用2辆小客车和1辆大客车,则每次可运送学生95人;若用1辆小客车和2辆大客车,则每次可运送学生115人(注意:每辆小客车和大客车都坐满).
(1)每辆小客车和大客车各能坐多少人?
(2)若现在要运送500名学生,计划租用小客车
 辆,大客车
辆,大客车 辆,一次送完,且恰好每辆车都坐满,请你帮学校设计出所有的租车方案.
辆,一次送完,且恰好每辆车都坐满,请你帮学校设计出所有的租车方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个形状、大小完全相同的含有
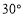 、
、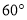 的直角三角板如图①放置,
的直角三角板如图①放置,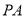 、
、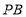 与直线
与直线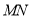 重合,且三角板
重合,且三角板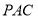 、三角板
、三角板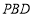 均可绕点
均可绕点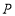 逆时针旋转.
逆时针旋转.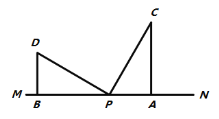
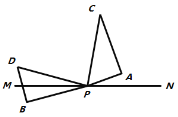
图① 图②
(1)直接写出
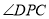 的度数是______.
的度数是______.(2)如图②,在图①基础上,若三角板
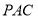 的边
的边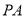 从
从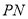 处开始绕点
处开始绕点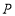 逆时针旋转,转速为4.5度/秒,同时三角板
逆时针旋转,转速为4.5度/秒,同时三角板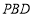 的边
的边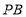 从
从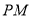 处开始绕点
处开始绕点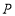 逆时针旋转,转速为0.5度/秒,(当
逆时针旋转,转速为0.5度/秒,(当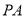 转到与
转到与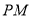 重合时,两三角板都停止转动),在旋转过程中,当
重合时,两三角板都停止转动),在旋转过程中,当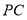 与
与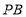 重合时,求旋转的时间是多少?
重合时,求旋转的时间是多少?(3)在(2)的条件下,
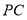 、
、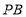 、
、 三条射线中,当其中一条射线平分另两条射线的夹角时,请求出旋转的时间.
三条射线中,当其中一条射线平分另两条射线的夹角时,请求出旋转的时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】一名考生步行前往考场,5分钟走了总路程的
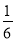 ,估计步行不能准时到达,于是他改乘出租车赶往考场,他的行程与时间关系如图所示(假定总路程为1,出租车匀速),则他到达考场所花的时间比一直步行提前了________分钟。
,估计步行不能准时到达,于是他改乘出租车赶往考场,他的行程与时间关系如图所示(假定总路程为1,出租车匀速),则他到达考场所花的时间比一直步行提前了________分钟。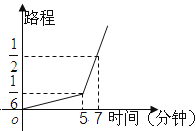
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上,已知点
 ,
, 分别表示数1,
分别表示数1, ,那么数轴上表示数
,那么数轴上表示数 的点应落在( )
的点应落在( )
A.点
 的左边B.线段
的左边B.线段 上C.点
上C.点 的右边D.数轴的任意位置
的右边D.数轴的任意位置 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
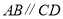 ,
,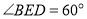 ,
,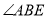 的平分线与
的平分线与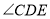 的平分线交于点
的平分线交于点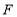 ,则
,则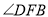 的度数是________.
的度数是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线
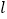 平行于直线EC,且直线
平行于直线EC,且直线 与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线
与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线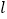 上, 则DF的长为_____
上, 则DF的长为_____
相关试题

